ИССЛЕДОВАНИЕ ДВИЖЕНИЯ УПРУГОЙ СИСТЕМЫ
| A spring is attached to a support, the ceiling if you will. A weight is attached to the end and the spring bobs up and down for a while, eventually settling down, as shown here.
|
| Consider a vertical axis whose origin is the weight's position when the spring is at rest, with the positive axis down. If the spring is set in vertical motion at time t = 0, the differential equation describing the spring's position along the vertical axis is given by
|
| is the position of the spring at time t.
|
| is the mass of the attached weight.
|
| is a drag coefficient. The term
|
| represents a retardation of motion that is proportional to velocity. b(t) is usually a constant reflecting air resistance or friction caused by the surrounding medium.
|
| is an external force acting on the spring at time, t.
|
| is the initial velocity of the spring.
|
| We'll solve the spring problem as a function of these parameters.
|
| We use rkfixed to solve the problem, illustrating some possible types of behavior.
|
| That's not too exciting . . . but it is correct. With no external force or initial velocity, the spring never gets started.
|
| Here we'll add a nonzero initial velocity and compute three solutions: one where the retarding force is 0, one where it is a nonzero constant, and one where the force is present only for a short time.
|
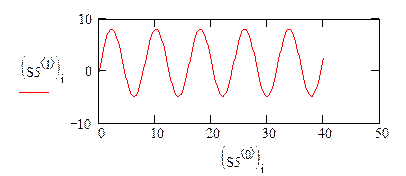
| The three solutions are graphed together below. Note that if there is no external force and no retarding force, the spring just bounces back and forth forever. Once the retarding force is added, the motion decays as you would expect. In the case of the initial retarding force, the motion is damped at the start but then the spring oscillates forever.
|
| Now let's vary the external force factor, keeping the retarding force at 0.
|
| Now, a steadily increasing force:
|
| Keep in mind, with this example and others where the solution appears unbounded, the position of the spring is in fact bounded by the actual length the spring can physically be stretched. The differential equation does not take this into account and models an infinitely stretchable spring.
|
| A steadily increasing force in the opposite direction:
|
| A constant force alternating in direction:
|
| By adjusting the floor expression in the above example, we can adjust the frequency of the applied force to be in sync with the frequency of the spring. We did this here.
|
| Finally, a random force :
|
| Лабораторная работа № 5
Решение систем ДИФФЕРЕНЦИАЛЬНЫХ уравнений
|
| At integer values F has the value 100, but it is 0 everywhere else:
|
| You can think of this as a spring problem where at every unit of time a force of 100 units is applied to the weight at the end of the spring.
|
| Looks good, but does it reflect the ODE we're trying to solve? The answer is no. Here's why.
|
| We used a fixed step size routine on the interval
|
| points. This requires a step size of
|
| With that nice step size and a starting value of 0, you would expect to land on an integer value every 20 steps. A look at the time output reveals
|
| So, this is apparently true.
|
| But, if we compute F at these values, we see
|
| F is not 100 at every one of these “integer” values as it should be!
|
| The culprit here is our old friend round-off error. A closer look at the integer values shows that our steps missed some of the integer values. Very close, but no cigar!
|
| Thus, the full effect of our force factor does not appear in the solution to our ODE.
|
| But, the real problem here is not so much the round-off error but the sensitivity of our function, F, to values that are extremely near an integer.
|
putting in a threshold (  ) at which we're willing to say something is an integer. Then ) at which we're willing to say something is an integer. Then
|
| That's good. Furthermore, our step size of
|
| is much larger than our threshold. So, while stepping no point will evaluate to 100 that shouldn't.
|
return false">ссылка скрыта
| Comparing the two solutions
|
| we find that the two solutions agree initially where the force was being detected in both solutions, but diverge later since the new solution is feeling the force.
|
| Лабораторная работа № 6
ИССЛЕДОВАНИЕ КИНЕМАТИКИ ЭКСКАВАТОРА
SmartSketch: Mathcad-Driven Backhoe Drawing
|
| This worksheet uses Mathcad to control the position of a backhoe arm in a SmartSketch drawing.
|
| Note: This worksheet contains a screenshot of a SmartSketch component. The working file is located in the CAD\SmrtSkch subfolder of the Samples directory.
|
| Change the value of case to 1, 2, 3, 4 or 5 to control the position of the arm and watch the drawing automatically update.
|
| This program is “globally defined” so that Mathcad recognizes its existence at the top of the document.
|
Литература
1. Заварыкин В.М., Житомирский В.Г., Лапчик М.П. Численные методы. М.: Просвещение. – 1991. – 175с.
2. Ракитин В.И., Первушин В.Е. Практическое руководство по методам вычислений. М.: Высшая школа. – 1998. 384с.
3. Волков Е.А. Численные методы. М.: Наука. – 1987. – 248 с.
3. Турчак Л.И. Основы численных методов. М.: Наука. – 1987. – 318с.
4. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. М.: Наука. – 1972. – 366с.
5. Березин И.С., Жидков Н.П. Методы вычислений. Т.1. М.: Наука. – 1966. – 632с.
6. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М. – С.П.: Физматлит. – 2001. – 630с.
7. С. Ф. Аминова, Р. М. Асадуллин. Лабораторный практикум по курсу «Численные методы».- Уфа: Изд-во БГПУ, 2003 –28с.
8. Р. Р. Сулейманов. Решение математических задач в системе MathCAD 8.1 // Учитель Башкортостана. 2002. № 2.
10. MATHCAD 6.0 PLUS/ Финансовые, инженерные и научные расчеты в среде Windows 95./ Пер. с англ. – М.: Информационно-издательский дом "Филинъ", 1996. – 712 с.
11. Плис А.И., Сливина Н.А. Mathcad: математический практикум. – М.: Финансы и Статистика. – 1999.
12. Очков В.Ф. Mathcad 8 Pro для студентов и инженеров. – М.: КомпьютерПресс, 1999.
13. Очков В.Ф.. MathCad 7 Pro для студентов и инженеров. – М.: КомпьютерПресс, 1998. – 384 с.
14. Дьяконов В.П. Справочник по MathCAD PLUS 6.0 PRO. – М.: CK Пресс, 1997. – 336 с.




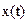

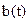










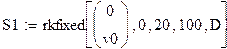











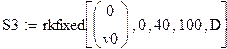


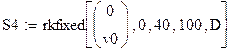

































































 ) at which we're willing to say something is an integer. Then
) at which we're willing to say something is an integer. Then











