Алгоритм Брезенхема.

Простой пошаговый алгоритм

позиция = начало

шаг = приращение

1. ifпозиция - конец < точность then4

if позици > конец then 2

ifпозиция < конец then 3

2. позиция = позиция - шаг

go to 1

3. позиция = позиция + шаг

go to 1

4. finish

Хотя алгоритм Брезенхема был первоначально разработан для цифровых графопостроителей, однако он в равной степени подходит для использования растровыми устройствами с ЭЛТ. Алгоритм выбирает оптимальные растровые координаты для представления отрезка. В процессе работы одна из координат - либо x, либо y (в зависиимости от углового коэффициента) - изменяется на единицу. Изменение другой координаты (на 0 или 1) зависит от расстояния между действительным положением отрезка и ближайшими координатами сетки. Такое расстояние мы назовем ошибкой.

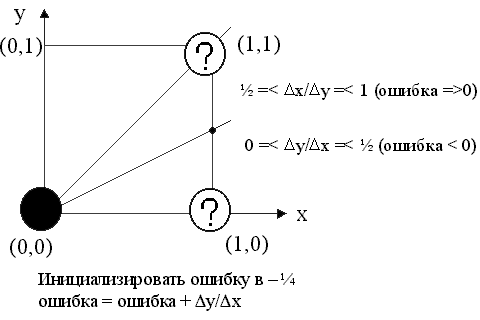
Алгоритм построен так, что требуется проверить лишь знак этой ошибки. На рис.3.1 это иллюстрируется для отрезка в первом октанте, т.е. для отрезка с угловым коэффициентом, лежащим в диапазоне от 0 до 1. Из рисунка можно заметить, что если угловой коэффициент отрезка из точки (0,0) больше, чем 1/2, то пересечение с прямой x = 1 будет расположено ближе к прямой y = 1, чем к прямой y = 0. Следовательно, точка растра (1,1) лучше аппроксимирует ход отрезка, чем точка (1,0). Если угловой коэффициент меньше 1/2, то верно обратное. для углового кэффициента, равного 1/2, нет какого либо предпочтительного выбора. В данном случае алгоритм выбирает точку (1,1).

Рис. 3.1. Основная идея алгоритма Брезенхема.

Не все отрезки проходят через точки растра. Подобная ситуация иллюстрируется рис.3.2, где отрезок с тангенсом угла наклона 3/8 сначала походит через точку растра (0,0) и последовательно пересекает три пиксела. Также иллюстрируется вычисление ошибки при представлении отрезка дискретными пикселами.

Рис.3.2. График ошибки в алгоритме Брезенхема.

Так как желательно проверять только знак ошибки, то она первоначально устанавливается равной -1/2. Таким образом, если угловой коэффициент отрезка больше или равен 1/2, то величина ошибки в следующей точке растра с координатами (1,0) может быть вычислена как

e = e + m

где m - угловой коэффициент. В нашем случае при начальном значении ошибки -1/2

e = 1/2 + 3/8 = -1/8

Так как е отрицательно, отрезок пройдет ниже середины пиксела. Следовательно, пиксел на том же самом горизонтальном уровне лучше аппроксимирует положение отрезка, поэтому у не увеличивается. Аналогично вычисляем ошибку

e = -1/8 + 3/8 = 1/4

в следующей точке растра (2,0). Теперь е положительно, значит отрезок пройдет выше средней точки. Растровый элемент (2,1) со следующей по величине координатой у лучше аппроксимирует положение отрезка. Следовательно у увеличивается на 1. Прежде чем рассматривать следующий пиксел, необходимо откорректировать ошибку вычитанием из нее 1. Имеем

e = 1/4 - 1 = -3/4

Заметим, что пересечение вертикальной прямой x = 2 с заданным отрезком лежит на 1/4 ниже прямой у = 1. Еслиже перенести отрезок 1/2 вниз, мы получим как раз величину -3/4. Продолжение вычислений для следующего пиксела дает

e = -3/4 + 3/8 = -3/8

Так как е отрицательно, то у не увеличивается. Из всего сказанного следует, что ошибка - это интервал, отсекаемый по оси у рассматриваемым отрезком в каждом растровом элементе (относительно -1/2).

Приведем алгоритм Брезенхема для первого октанта, т.е. для случая 0 =< y =< x.

Алгоритм Брезенхема разложения в растр отрезка для первого октанта

предполагается, что концы отрезка (x1,y1) и (x2,y2) не совпадают

Integer - функция преобразования в целое

x, y, x, y - целые

е - вещественное

инициализация переменных

x = x1

y = y1

x = x2 - x1

y = y2 - y1

Инициализация с поправкой на половину пиксела

е = y/x - 1/2

начало основного цикла

for i = 1 to x

plot (x,y)

while ( e => 0 )

y = y + 1

e = e - 1

end while

x = x + 1

e = e + y/x

next i

finish

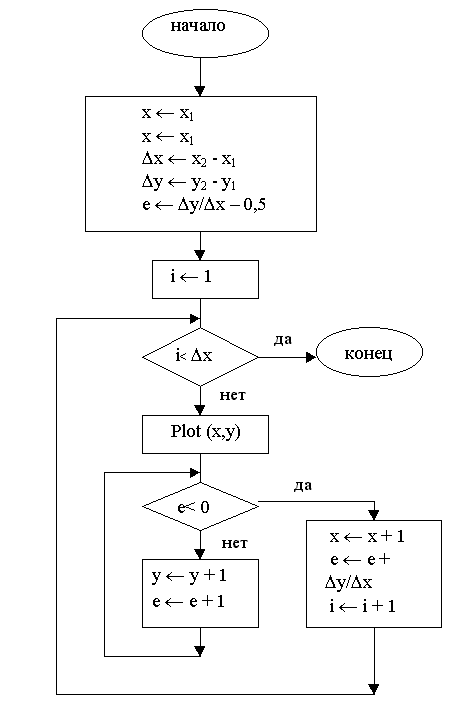
Блок-схема алгоритма приводится на рис.3.3. Пример приведен ниже.

Рис. 3.3. Блок-схема алгоритма Брезенхема.

Пример 3.1. Алгоритм Брезенхема.

Рассмотрим отрезок проведенный из точки (0,0) в точку (5,5). Разложение отрезка в растр по алгоритму Брезенхема приводит к такому результату:

начальные установки

x = 0

y = 0

x = 5

y = 5

е = 1 - 1/2 = 1/2

результаты работы пошагового цикла

i	Plot	e	x	y
		1/2
	(0,0)
		-1/2
		1/2
	(1,1)
		-1/2
		1/2
	(2,2)
		-1/2
		1/2
	(3,3)
		-1/2
		1/2
	(4,4)
		-1/2
		1/2

Результат показан на рис.3.4 и совпадает с ожидаемым. Заметим, что точка растра с координатами (5,5) не активирована. Эту точку можно активировать путем изменения цикла for-next на 0 to x. Активацию точки (0,0) можно устранить, если поставить оператор Plot непосредственно перед строкой next i.

Рис. 3.4. Результат работы алгоритма Брезенхема в первом октанте.

В следующем разделе описан общий алгоритм Брезенхема.