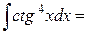Интегрирование некоторых тригонометрических выражений.
Краткие итоги
Управление памятью – одна из важнейших функций операционной системы, которая выполняет размещение в памяти пользовательских программ и их данных для их выполнения. Первоначально введенные в систему пользовательские программы помещаются во входную очередь на диске.
Связывание команд и данных с адресами в памяти может выполняться во время компиляции, во время загрузки или во время выполнения.
Пользовательская программа проходит следующие фазы обработки: из исходного кода – компиляция в объектный модуль, затем – генерация из нескольких объектных модулей загрузочного модуля (редактором связей); генерация из загрузочного модуля и библиотек загрузчиком двоичного образа программы в памяти (линковка).
Различаются логические и физические адреса. Логический адрес генерируется процессором при выполнении команд. Физический адрес генерируется устройством управления памятью как сумма логического адреса и значения регистра перемещения.
Устройство управления памятью – модуль аппаратуры, выполняющий преобразование логических адресов в физические и обращения по физическим адресам памяти.
Динамическая загрузка – загрузка вызываемой подпрограммы в память при первом ее вызове, при исполнении пользовательской программы. Динамическая линковка – линковка во время выполнения программы. Библиотеки подразделяются на статически и динамически линкуемые. Для динамической линковки в бинарном коде хранится заглушка, которая вызывает ОС для поиска и загрузки динамически линкуемой библиотеки, с последующей заменой кода заглушки на код обращения к библиотеке.
Оверлейная структура – метод организации программы, не помещающейся целиком в основную память, при котором программа при разработке делится на непересекающиеся группы модулей, необходимые одновременно в памяти, а при исполнении драйвер оверлея по очереди загружает в одну и ту же область памяти то одну, то другую группы модулей.
· Для нечётных степеней sinx или cosx применимо правило:
Правило 1:
Для вычисления интегралов вида:
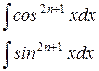
(n – целое положительное число) применим метод замены переменной – ввести вспомогательную функцию sinx в первом случае и cosx – во втором случае.
или, что то же самое применить метод внесения под знак дифференциала – выделим множитель cosx в первом случае и sinx – во втором случае и его внесём под знак дифференциала:
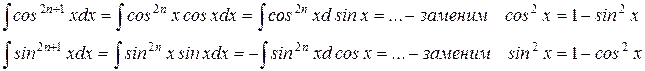
Пример 1:
метод прямой замены переменной:
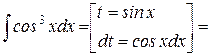
Пример 2:
метод внесения под знак дифференциала:
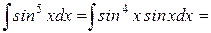
· Для чётных степеней sinx или cosx применимо правило:
Правило 2:
Для вычисления интегралов вида:
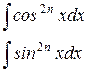
(n – целое положительное число) применим метод понижения степени по формулам:
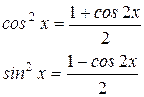
Пример 3:
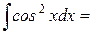
Пример 4:
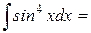
· Для произведений степеней sinx и cosx, в которых по крайней мере одна из степеней нечётна применимо правило:
Правило 3:
Для вычисления интегралов вида:
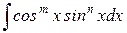
где по крайней мере одно из чисел m, n – нечётное, применим метод замены переменной – ввести вспомогательную функцию sinx, если n – нечётно и cosx, если m – нечётно.
или, что то же самое применить метод внесения под знак дифференциала, а именно, выделим множитель cosx, если m – нечётное и sinx, если n – нечётное и его внесём под знак дифференциала.
Пример 5:
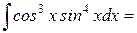
· Для произведений степеней sinx и cosx, в которых обе степени чётны применимо правило:
Правило 4:
Для вычисления интегралов вида:
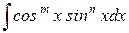
где оба числа m, n – чётны, применим метод понижения степени по формулам:
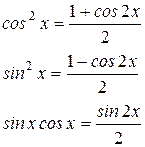
Пример 6:
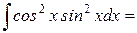
Пример 7:
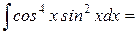
· Для произведений sinmx и cosnx, применимо правило:
Правило 5:
Для вычисления интегралов вида:
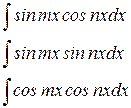
будем использовать формулы:
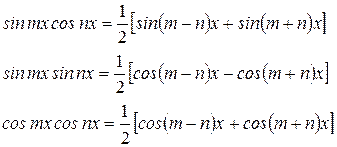
Пример 8:
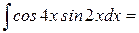
· Для степеней tgx или ctgx применимо правило:
Правило 6:
Для вычисления интегралов вида:
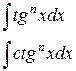
(n – целое число, большее 1) выделим множитель tg2x в первом случае и ctg2x – во втором случае и будем использовать формулы:
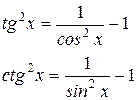
Пример 9:
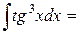
Пример 10: