Лазерные пучки высшего порядка.

Вывод.

 

1. Полученное путем вычислений выражение удовлетворяет уравнению Гаусса. (пучки типа ТЕМ₀₀)

 

При больших z: а(z)≈2a₀z/ka₀²=z/πa₀

Угол дифракционной расходимости: Θ=λ/πa₀

Поле расходится, а поток энергии остается тем же самым, площадь под кривыми равна.

 

2. Физическая интерпретация множителей, ответственных за фазу Гауссова пучка.

1) - изменение фазы соответствует однородной плоской бегущей волне.

2) - добавка к фазе (0,π/2), где ка₀²/2-фокальный параметр пучка. Для Гауссовых пучков не играет роли

3) - описывает фазу и характеризует искривление волнового фронта.

Величина - определяет радиус кривизны волнового фронта.

 

 

При z =>0 R(z)=>

При z=>R(z)=>z

Если рассматривать волновой фронт, то в т. z=0 он будет являться плоским, далее кривизна будет увеличиваться до некоторого z_min=ка₀²/2 (R_min=ka₀²), после чего опять уменьшаться.

Расходимость зависит от а₀.

Если взять z=0, то R(0)= , а(0)=а₀

Если известно значение z, то можно определить параметры а(z) и R(z) по формулам: , 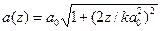. Независимыми являются только 2 параметра из 3, т.е. если заданы 2 произвольных параметра из 3-х, то пучок определяется однозначно.

3) !

(Гауссовские пучки высшего порядка, Гауссо-Эрмитовые пучки высшего порядка)

 

 

Волна обозначается как ТЕМ_mn, где m, n - индексы поперечного распределения (поперечной моды)

1) m- количество занулений поля вдоль оси х

2) n – количество занулений поля вдоль оси у

3) m+n - порядок пучка.

 

 

Распределение поля для Гауссо-Эрмитовых пучков (ТЕМ_mn), где m+n>0

 

=

 

Где Н – полиномы Эрмита:

Н0
Н1	2ξ
Н2	4ξ2-2
…	…

 

1) Предельный случай m=n=0, Н₀=1 – получается выражение для Гауссова пучка.

2) Если m0, n0:

ТЕМ₁₀

Наличие множителей Н_m и H_n объясняют данное распределение.

 

Угол дифракционной расходимости , коэффициент возрастает при увеличении порядка пучка (m+n).