Функциональная и алгоритмическая структуры амплитудно-импульсной системы

Рис. 1.13

Рис. 1.11

 

Экстраполятор – устройство, предназначенное для преобразования выходного сигнала ДФ в непрерывную величину, поступающую на вход НЧ. Экстраполяция сводится к построению непрерывной функции времени, значения которой близки для к значениям дискретного сигнала на выходе ДФ. Простейший способ преобразования - запоминание значений дискретного сигнала на всем периоде дискретности . Чаще всего выходные данные ЭВМ преобразуются в последовательность прямоугольных импульсов единичной скважности, рис. 1.12. При этом передаточная функция Э эквивалентна ФЭ, т.е.

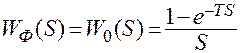- передаточная функция экстраполятора нулевого порядка.

 

Рис. 1.12

 

 

Эквивалентная схема цифровой системы управления, рис. 1.13.

 

 

Если коррекция осуществляется с помощью непрерывных устройств, то .

Исследование дискретной САУ можно приближенно свести к исследованию эквивалентной непрерывной системы, в которой совмещенность ИЭ и Э заменяется непрерывным звеном с передаточной функцией 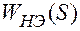и сумматором, на который помимо основного сигнала поступает помеха от эффекта квантования по времени входного сигнала, рис. 1.14.

 

Рис. 1.14

 

ДФ изменяет закон модуляции, рис. 1.15.

 

Рис. 1.15

 

В общем случае импульсный элемент может входить в состав любого функционального блока системы управления. Дискретный характер работы системы может быть обусловлен, например, ис­пользованием датчика периодического действия (различные ана­лизаторы состава вещества). Но в большинстве случаев дискрет­ность системы связана с наличием в ее контуре коммутирующих устройств МП и ДМП, которые периодически за­мыкают и разрывают цепь регулирования.

Рассмотрим типичную функциональную структуру импульсной системы (рис. 1.16, а). К такой структуре могут быть сведены почти все случаи включения импульсного элемента. Импульсные эле­менты ИЭ₁ и ИЭ₂, которые реально находятся в задатчике и обратной связи, могут быть учтены одним импульсным элементом ИЭ.

 

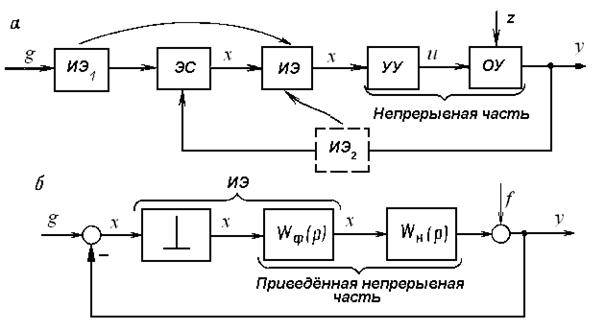
Рис. 1.16Функциональная (а) и алгоритмическая (б) структуры амплитудно-импульсной системы управления

Импульсный элемент ИЭ, осуществляющий в системе кванто­вание по времени, можно рассматривать как амплитудно-импульс­ный модулятор (рис. 1.16, а). Модулятор умножает несущий сигнал — последовательность одинаковых импульсов, поступающих с генератора импульсов ГИ, на модулирующий сигнал — входной непрерывный сигнал . Образующийся при этом на выходе ди­скретный сигнал 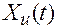представляет собой последовательность импульсов, амплитуды которых равны или пропорциональны мгно­венным значениям непрерывного сигнала.

Для упрощения анализа системы с АИМ целесообразно реаль­ный импульсный элемент ИЭ заменить эквивалентным последова­тельным соединением идеального импульсного элемента ИИЭ и фор­мирующего элемента ФЭ (рис. 1.17, б). Идеальный импульсный эле­мент преобразует непрерывный сигнал в последовательность мгновенных равноотстоящих друг от друга импульсов, площади которых равны значениям входного сигнала в дискретные моменты времени. Формирующий элемент или демодулятор образует из мгно­венных импульсов такие импульсы, которые по форме совпадают с импульсами на выходе реального импульсного элемента.

Реакция формирующего элемента на единичный импульс, т. е. на дельта-функцию, есть весовая функция 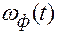этого элемента. Поэтому передаточная функция формирующего элемента:

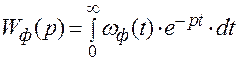, (1.1)

где - функция, описывающая импульс на выходе реального импульсного элемента при действии на входе дельта-функции.

Формирующий элемент является звеном непрерывного дейст­вия, и его при анализе удобно объединять с непрерывной частью системы (см. рис. 1.16, б).

Рис. 1.17 Алгоритмическая структура импульсного элемента

 

Образующееся при этом соединение на­зывается приведенной непрерывной частью системы. Передаточная функция приведенной непрерывной части.

. (1.2)

В наиболее часто встречающемся случае, когда несущие им­пульсы имеют прямоугольную форму, формирующий элемент дол­жен преобразовать единичную дельта-функцию в прямоугольный импульс с единичной высотой и длительностью , где — скважность или относительная длительность. Такой импульс можно представить в виде разности двух ступенчатых функций, сдвинутых на время , т. е.

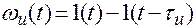. (1.3)

Отсюда, согласно (1.1), передаточная функция формирующего элемента

(1.4)

Если длительность импульсов , времени существенно меньше основных постоянных времени остальных звеньев непрерывной части си­стемы, то формирующий элемент (1.4) может быть приближенно заменен безинерционным звеном .

Рис. 1.18 Простейший квантователь и фиксатор.

 

При формирующий элемент (1.4) выдает в течение всего периода повторения Т постоянный сигнал, равный значению вход­ного сигнала в начале периода Т. Поэтому в данном частном (но распространенном) случае формирующий элемент называется фиксирующим или запоминающим. Передаточная функция фикси­рующего элемента

. (1.5)

Так как фиксацию мгновенного значения сигнала на постоян­ном уровне можно рассматривать как простейшую экстраполя­цию — экстраполяцию полиномом нулевого порядка, то формирую­щий элемент в указанном частном случае () называется также экстраполяторомнулевого порядка.

В качестве простейшего примера рассмотрим последовательно соединенные квантователь по времени К и запоминающий элемент ЗЭ, а также сигналы в этой цепи (рис. 1.18).

Так как квантователь по времени и запоминающий элемент яв­ляются важными частями дискретной системы, существенно влияю­щими на ее динамику, проанализируем их частотные свойства. Квантователь по времени или идеальный импульсный элемент можно рассматривать как генератор дополнительных гармоник, частота которых равна частоте дискретизации . Спектр сигнала , квантованного по времени по принципу АИМ, равен следующей сумме смещенных спектров непрерывного входного сигнала :

, (1.6)

где — спектр входного (квантуемого) сигнала (рис. 1.19, а). Очевидно, что при квантовании амплитуды всех гармоник умень­шаются в Т раз. Это означает, что импульсный элемент эквивален­тен по своим свойствам безынерционному звену с передаточным коэффициентом 1/T.

 

Рис. 1.19 Амплитудные спектры входного и выходного сигналов идеального квантователя и а.ч.х. фиксатора

 

В общем случае спектр существенно отличается от спектра : он содержит как основную составляющую (k = 0), совпадающую с , так и дополнительные составляющие (k = ± 1; ± 2; . . .), возникающие при квантовании.

Если ширина спектра квантуемого сигнала , то до­полнительные составляющие в основном диапазоне частот не искажают форму спектра (рис. 1.19, б), т. е.

. (1.7)

Если частота квантования недостаточно велика и , то в основном диапазоне спектр искажается прилегающими составляющими с k ± 1 (рис. 1.19, в).

Таким образом, на основе проведенных физических рассужде­ний можно сформулировать теорему о квантовании:

если непрерывный сигнал обладает спектром, ограниченным частотой , то его квантование по времени с частотой не приводит к потере информации, т. е. сигнал однозначно и полностью представляется своими дискретными значениями, взятыми через интервал квантования

.

Строгое доказательство этой теоремы было дано советским уче­ным-радиотехником В.А. Котельниковым в 1933 г. и американ­ским математиком К. Шенноном в 1949 г.