Какие задачи решают корректирующие устройства?

Контрольные вопросы к лекции 1

Рис.4.22.Реализация передаточной функции

Рис.4.21. Логарифмическая амплитудная характеристика

Рис.4.18.Контур последовательного корректирующего устройства

Рис.4.14.Вещественная характеристика

Рис.4.13. Определение связи частоты среза с оценками качества переходного процесса

Рис.4.12.Определение связи частоты среза с оценками качества переходного процесса

Рис.4.11. Оптимизация переходного процесса

Рис.4.10.Т-образные мостовой и двойной корректирующие звенья

Рис.4.9.Дифференцирующее и интегрирующее звенья

Рис.4.8.Схемы включения корректирующих устройств в схему

Рис.4.7.Коррекция ЛАЧХ

Рис.4.6.Коррекция с помощью интегродифференцирующих звеньев

Рис.4.5. Коррекция логарифмических амплитудно-частотных характеристик

Рис.4.4.Коррекция с помощью интегрирующего звена

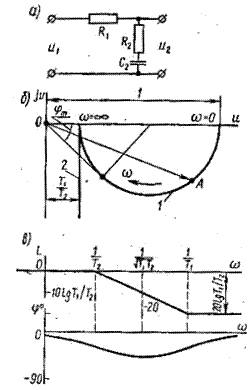
Рис.4.2.Пассивное дифференцирующее звено в прямой цепи системы

Рис.4.1.Коррекция с помощью дифференцирующих устройств

Раздел 4. Лекция 1. Синтез корректирующих устройств и улучшение качества процесса регулирования

Привидите примеры переходных процессов при работе системы в режиме стабилизации.

Привидите пример построения АФХ объекта.

На примере АФХ САУ покажите, что такое запас устойчивости по модулю и по фазе.

Дайте определение синтезу и анализу САУ.

Дайте определение идентификации объекта.

4.Как решается задача идентификации объекта?

8.Что такое статическая настройка?

9.Что такое динамическая настройка?

Литература по лекции 4.

1.Ульянов В,А., Святов В.В., Ларин М.А. Автоматизация производственных процессов: Метод. Указание по курсовому и дипломному проектированию. Ч.1. Н.Новгород: НГТУ, 1997. –54 с..

3.Майзель М.М. Автоматика, телемеханика и системы управления производственными процессами. М.: М.: Высшая шкала, 1972. С.203-264.

4.Воронов А.А., Титов В.К., Новогранов Б.Н. Основы теории автоматического регулирования и управления. М.: Высшая школа, 1977. С.200-313.

5.Коганов В.Ю., Блинов О.М., Беленький А.М. Автоматизация управления металлургическими процессами. М.: Металлургия, !974. С.33-71.

7.Дорф Р., Бишоп Р. Современные системы управления. М.: Лаборатория Базовых Знаний, 2002. С.55-192, 349-564.

8.Филипс Ч., Харбор Р. Системы управления с обратной связью. М.: Лаборатория Базовых знаний, 2001. С.113-381.

9.Методы классической и современной теории автоматического управления. Т.1/Под ред. К.А. Пупкова. М.: МГТУ, 2004. С.68-119, 143-189.

При проектировании автоматических систем приходится решать задачи, как обеспечение устойчивости и качества процесса регулирования, имеющие противоречивый характер. Удовлетворительное решение первой задачи, соответствующее нужному запасу устойчивости, может привести к неудовлетворительным характеристикам в переходном процессе или в установившемся режиме. Возможен и противоположный случай, когда реализация требуемых характеристик качества, например связанная с повышением точности в установившемся режиме, сопровождается чрезмерным понижением запаса устойчивости. Противоречие между двумя задачами особенно наглядно проявляется, если делается попытка решить их одним и тем же способом. Например, уменьшение ошибок в установившемся режиме методом повышения коэффициента усиления в разомкнутой системе, как правило, приводит к уменьшению запаса устойчивости. Метод, используемый для повышения статической точности, - повышение порядка астатизма – также неблагоприятно сказывается на устойчивости, уменьшая запас устойчивости и увеличивая колебательность процесса.

Удовлетворительное решение задачи реализации как требуемого запаса устойчивости, так и качества процесса регулирования может быть достигнуто при одновременном использовании упомянутых методов и изменении структуры системы или включении корректирующих устройств в прямую цепь внутренней обратной связи. Основное назначение корректирующего устройства – изменение динамических свойств системы в направлении желаемых характеристик, что проявляется в изменении усиления по отдельным гармоникам или только в той области частот, которая оказывается существенной в той области частот, которая оказывается существенной для формирования той или иной динамической характеристики. Влияние корректирующего устройства на динамические свойства системы проявляется также и в изменении фазовой характеристики.

Использование корректирующих устройств наряду с изменением коэффициента усиления в разомкнутой цепи и изменением порядка астатизма приводит в конечном итоге к деформации частотных характеристик, что определяет коррекцию динамических свойств системы.

Физическая основа коррекции состоит в следующем. Динамические свойства системы необходимо изменить с помощью корректирующих устройств таким образом, чтобы приблизить их к желаемым. В этом случае обеспечиваются условия, при которых исполнительный элемент посредством управляющего звена вырабатывает сигнал управления (вращающий момент или силу тяги). Сигнал управления содержит составляющие, которые оказывают влияние на те или иные качественные показатели процесса регулирования. Так, например, применение дифференцирующих корректирующих устройств в прямой цепи системы позволяет осуществить дифференцирование сигнала ошибки и получить составляющую во вращающем моменте исполнительного элемента, пропорциональную скорости изменения рассогласования. Эта составляющая оказывает стабилизирующее действие на колебания в переходном процессе. Использование в прямой цепи интегрирующих корректирующих устройств приводит к интегрированию сигнала ошибки и получению составляющей во вращающем моменте (или силе тяги) исполнительного элемента, пропорциональной интегралу ошибки по времени. Эта составляющая момента (или силы) действует на ошибку в установившемся режиме в направлении её уменьшения до нуля. При ошибке, отличной от нуля, интегральная составляющая момента с течением времени с течением времени будет возрастать, что вызовет ускорение выходного звена системы и уменьшение ошибки.

Рассмотрим методы коррекции динамических свойств, которые находят применение в практике.

Коррекция с помощью дифференцирующих устройств. Дифференцирующие звенья, включаемые последовательно в прямую цепь системы регулирования, применяют в тех случаях, когда необходимо увеличить частоту среза или полосу пропускания этой системы, не уменьшая запаса устойчивости. Простейшей схемой, которая обеспечивает подобную коррекцию, является схема, приведённая на рис.4.1, и состоящая из RC-элементов.

Передаточная функция RC-контура

где .

Амплитудно–фазовая характеристика дифференцирующей цепи, соответствующая передаточной этой функции, построена по выражению

и показана на рис.4.1, б в виде полуокружности 1. При этом выражения для действительной и мнимой частей имеет вид

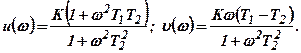
Если исключить частоту 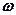и полученные уравнения преобразовать к виду

то последнее уравнение будет определять полуокружность в квадрате I с центром на действительной оси, находящимся на расстоянии 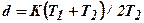от начала координат, и радиусом 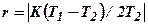. При изменении это уравнение соответствует полуокружности, представленной на рис.4.1, б, так как в рассматриваемом случае 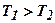и мнимая часть 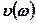принимает только положительные значения. Вектор при этом скользит по полуокружности 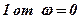до 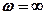, начиная и кончая своё движение на действительной оси. Для сравнения на рис.4.1, б изображена АФХ 2, соответствующая типовому дифференцирующему звену с передаточной функцией .

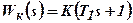Характеристика показывает, что пассивная RC-цепь (рис.4.1, а) в диапазоне частот вносит только опережение по фазе. Характеристика (рис.4.1, б) ближе всего подходит к идеальной характеристике 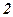в области низких частот. Однако точность дифференцирования для коррекции динамических свойств системы большого значения не имеет. Важно то, что цепь даёт опережение по фазе и в этом отношении обладает свойством идеальных дифференцирующих устройств. Максимальное фазовое опережение будет иметь место тогда, когда вектор займёт положение касательной к окружности , т.е. при .

На рис.4.1, в приведён логарифмические характеристики, соответствующие рассматриваемому RC- контуру. Логарифмическая АЧХ представлена ломанной, у которой асимптота в диапазоне частот 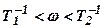имеет наклон +20 дБ/дек. Фазочастотная характеристика располагается в области положительного значения аргумента. Это свидетельствует о том, что RC-контур даёт опережение по фазе. Как видно из графика, особенностью пассивной дифференцирующей цепи является уменьшение усиления на низких частотах и повышение чувствительности к помехам на высоких частотах. Вследствие этого дифференцирующие звенья подвержены влиянию помех, что является их недостатком.

Включение пассивного дифференцирующего звена в прямую цепь системы (рис.4.2) снижает общий коэффициент усиления. Если скомпенсировать это ослабление, увеличив, например, коэффициент усиления К_у усилителя, то коррекция дифференцирующим контуром позволяет увеличить полосу пропускания и быстродействие системы, не уменьшая запаса устойчивости. На рис.4.3 для примера показана коррекция дифференцирующей схемой в случае, когда передаточная функция нескорректированной системы определяется формулой

Рис.4.3. Пример коррекции дифференцирующей схемой.

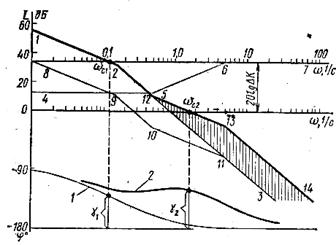Логарифмические АЧХ И ФЧХ разомкнутой нескорректированной системы имеют вид ломанной 1-2-3 и кривой 1 соответственно. Асимптота 1-2 имеет наклон – 20 дБ/дек, а асимптота 2-3 – наклон – 40 дБ/дек. Частота среза определяется величиной , а запас устойчивости по фазе равен .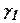

ЛАЧХ дифференцирующего контура при выбранных постоянных времени представлена ломанной 4-5-6-7. Так как корректирующее устройство включается последовательно в прямую цепь системы, то результирующая ЛАХ будет определяться суммой ординат характеристик 1-2-3 и 4-5-6-7 и, следовательно, будет иметь вид асимптотической характеристики 8-9-10-11-3. ЛФЧХ благодаря вносимому корректирующим контуром опережению по фазе определяется теперь кривой 2. Скомпенсировав уменьшение коэффициента усиления таким образом, чтобы асимптота 8-9 совпала с асимптотой 1-2, получим характеристику 1-2-12-13-14, которая свидетельствует об увеличении усиления на высоких частотах (заштрихованный участок на рис.3.65). Можно увеличить коэффициент усиления ещё на 20lgΔK и сделать частоту среза равной при запасе устойчивости по фазе 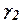. Который не меньше первоначального значения .

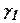Таким образом, коррекция с помощью дифференцирующих устройств позволяет без уменьшения запаса устойчивости увеличить частоту среза, а следовательно полосу пропускания и быстродействие системы. Одновременно увеличенное значение коэффициента усиления уменьшает ошибки в установившемся режиме.

При использовании этого метода коррекции большее увеличение коэффициента усиления на высоких частотах усиливает влияние помех на процесс регулирования. Этот недостаток следует иметь в виду, особенно в тех случаях, когда уровень помех велик.

Коррекция с помощью интегрирующих устройств. Применение интегрирующих звеньев для коррекции динамических свойств системы при последовательном включении их в прямую цепь обусловлено возможностью без уменьшения запаса устойчивости и практически без заметного изменения частоты среза поднять коэффициент усиления на низких частотах и тем самым существенной уменьшить ошибки в установившемся режиме.

На рис.4.4, а приведена интегрирующая RC-цепь, передаточная функция которой

где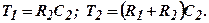

АФХ, соответствующая последнему уравнению представлена на рис.4.4, б в форме полуокружности 1, отвечающей уравнению , в котором следует положить К=1. Так как , то при изменении мнимая часть 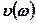будет принимать только отрицательные значения и последнее уравнение определяет полуокружность в IV квадранте.

Из графика видно, что интегрирующая цепь в диапазоне частот вносит только отставание по фазе, которое становится максимальным на частоте и равным углу 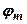между касательной к окружности 1 и положительным направлением действительной оси. Сравнение характеристики 1 с идеальной характеристикой 2, соответствующей звену с передаточной функцией 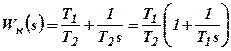, показывает, что в области высоких частот имеется наибольшее сближение характеристик. Однако, как и в предыдущем случае, наиболее важным при коррекции динамических свойств является не точность интегрирования, а наличие отрицательного фазового сдвига.

Логарифмические характеристики (рис.4.4, в) интегрирующего контура особенно наглядно показывают, что контур уменьшает усиление на высоких частотах при увеличении его на низких. Последнее иллюстрируется рис.4.5.

Нескорректированная система имеет ЛАХ 1-2-3 и фазочастотную характеристику 1. При частоте среза имеет запас устойчивости по фазе 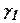. Для увеличения коэффициента усиления на низких частотах без существенного уменьшения запаса устойчивости по фазе необходимо, чтобы частота сопряжения 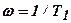, определяемая наименьшей из постоянных времени контура, была ниже частоты на 2-3 октавы. С учётом сказанного на рисунке построена ЛАХ 4-5-6-7 интегрирующего устройства. После суммирования характеристик 1-2-3 и 4-5-6-7 получим ЛАХ 1-8-9-10-11. Компенсируя ослабление усиления на высоких частотах, найдём ЛАХ 12-13-14-2-3 скорректированной системы, которой соответствует Фазочастотная характеристика 2. Заштрихованная часть указывает на увеличение коэффициента усиления в области низких частот. Это достигнуто без существенного изменения запаса устойчивости по фазе и частоты среза. Увеличение коэффициента усиления в низких частотах уменьшает ошибки в установившемся режиме и тем самым повышает статическую точность системы.

При коррекции с помощью интегрирующих устройств системы в меньшей мере подвержена влиянию помех.

Коррекция с помощью интегродифференцирующих устройствприменяется в тех случаях, когда необходимо, не уменьшая запаса устойчивости, увеличить частоту среза и полосу пропускания системы за счёт введения опережения по фазе и увеличения коэффициента усиления на высоких частотах, а также уменьшить ошибки в установившемся режиме, увеличивая коэффициент усиления на низких частотах.

Примером интегродифференцирующего контура может служить схема, показанная на рис.4.6, а. Передаточная функция этой цепи

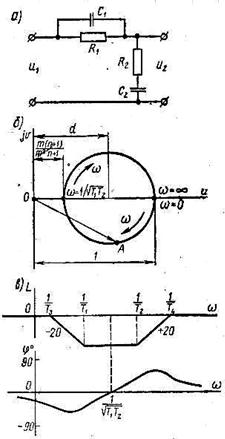
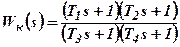где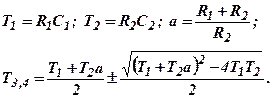

Если ввести обозначения для отношений постоянных времени 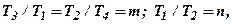то нетрудно показать, что АФХ рассматриваемой цепи

будет представлена окружностью (рис.3.68, б)

центр которой находится на действительной оси и смещён относительно начала координат на величину

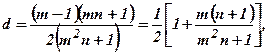а радиус .

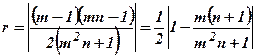При изменении 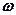в диапазоне 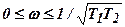конец вектора 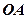скользит по полуокружности, расположенной под действительной осью, и контур вносит отставание по фазе. При дальнейшем увеличении частоты от 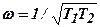до вектор скользит по полуокружности, расположенной над осью абсцисс, что соответствует введению дифференцирующего эффекта, т.е. опережению по фазе.

На рис.4.6, в приведены логарифмическая амплитудно – частотная 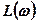и Фазочастотная 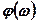характеристики интегродифференцирующего контура. Как следует характеристик, контур даёт ослабление усиления на средних частотах. Компенсация этого ослабления совместно с возможностью увеличения коэффициента усиления благодаря введению опережения по фазе на высоких частотах позволяет значительно поднять коэффициент усиления системы.

На рис.4.7 показаны ЛАХ 1-2-3 и соответствующая фазочастотная характеристика 1 нескорректированной системы. При частоте среза имеет запас устойчивости по фазе 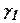. Асимптотическая характеристика 4-5-6-7-8-9 определяется интегродифференцирующим устройством. Суммируя ординаты ломанных, получим характеристику 1-10-11-12-3. Компенсируя ослабление усиления на средних частотах, получим ЛАХ 13-14-15-16-17. Этой характеристике, а также характеристике 1-10-11-12-3 соответствует фазовая характеристика 2. Очевидно, имеется возможность без заметного уменьшения запаса устойчивости по фазе ещё более увеличить коэффициент усиления до величины, при которой частота среза станет равной , имея запас устойчивости по фазе 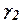, приблизительно равный исходной величине 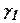в нескорректированной системе.

Коррекция интегродифференцирующим звеном позволяет уменьшить ошибки в установившемся режиме и увеличить быстродействие системы, т.е. уменьшить время переходного процесса, не уменьшая запаса устойчивости.

Коррекция динамических свойств с помощью обратных связей.

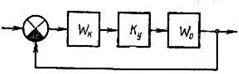
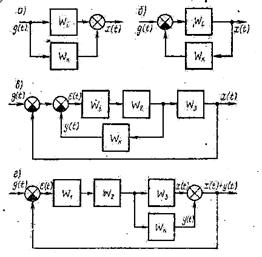Существует два способа включения параллельных корректирующих устройств в схему. Один способ предполагает прямое параллельное включение звеньев (рис.4.8, а). При использовании второго способа корректирующее звено 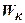включается в цепь обратной связи, которой охватывается одно или несколько основных звеньев 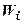прямой цепи (рис.4.8, б). Однако в замкнутой системе различие между названными способами становится условным, так как по отношению к одним звеньям корректирующее устройство включено по схеме, приведённой на рис.4.8, б, а по отношению к другим звеньям – по схеме, приведённой на рис.4.8, а. Это можно проиллюстрировать на структурных схемах того же рисунка. На рис.4.8, в корректирующее звено образует внутреннюю обратную связь, которой охватываются звенья 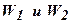прямой цепи. Пользуясь правилами преобразования структурных схем и рассматривая в качестве выходного сигнала величину 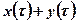, можно получить структурную схему (рис.4.8, г), в которой то же корректирующее звено по отношению к элементу 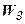прямой цепи включено по схеме, приведённой на рис.4.9, а. Учитывая это, при изложении основ метода параллельной коррекции будем рассматривать только обратные связи.

Внутренние обратные связи могут быть как положительными, так и отрицательными. Положительная обратная связь применяется для увеличения коэффициента усиления в той части системы, которая охватывается ею. С помощью отрицательных обратных связей можно уменьшить постоянные времени и изменить тип звена. Среди отрицательных обратных связей различают жёсткую и гибкую обратные связи.

Передаточная функция для схемы, приведённой на рис.4.9, б, имеет вид

где знак «+» в знаменателе соответствует отрицательной обратной связи, а знак «-« - положительной.

Обратная связь называется жёсткой, если действует и в установившемся, и в переходном режимах. При этом передаточная функция корректирующего устройства может определяться усилительным звеном либо инерционным:

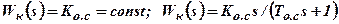В первом случае связь называется жёсткой, а во втором – инерционной жёсткой.

Обратная связь называется гибкой, если действует только в переходном режиме. Это возможно, когда передаточная функция параллельного корректирующего устройства определяется дифференцирующими элементами:

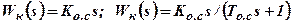Для первой из последних функций обратная связь называется идеальной гибкой.

Для второй передаточной функции, соответствующей реальному дифференцирующему элементу, обратная связь называется инерционной гибкой или изодромной.

Внутренние отрицательные обратные связи позволяют путём изменения динамических свойств звена, которое они охватывают (включением соответствующего устройства в цепь обратной связи), воздействовать на усиление, вводя опережение или отставание по фазе в том или ином диапазоне частот так же, как это имело место в случае последовательных корректирующих устройств.

Пусть усилительное звено с коэффициентом усиления К_i включается последовательно с интегрирующим контуром, схема которого приведена на рис.4.9, а. Передаточная функция этой последовательной комбинации 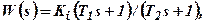где 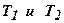определяются формулами, соответствующими выражению .

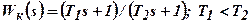Если необходимо, чтобы усилительное звено с передаточной функцией

, охваченное отрицательной обратной связью (рис.4.9, б), обладало передаточной функцией и свойствами интегрирующей цепи (см. рис.4.6, а), нужно выполнить условие

откуда находится передаточная функция параллельного корректирующего устройства: .

Подобное корректирующее устройство реализуется дифференцирующей цепью, показанной на рис.4.9, а. Для такого дифференцирующего контура

Чтобы два последних выражения были равными, нужно при одинаковых ёмкостях выбрать сопротивления и в соответствии с равенствами

Таким образом, включение в цепь обратной связи дифференцирующего звена придало схеме на рис.4.9, б свойства интегрирующей цепи. Усилительное звено совместно с гибкой инерционной обратной связью превратилось в звено интегрирующего типа. Гибкая инерционная обратная связь может быть использована для коррекции динамических свойств системы интегрирующими устройствами, так же как это имело место при последовательной коррекции.

В случае, когда усилительное звено с параллельным корректирующим устройством должно обладать дифференцирующими свойствами последовательной цепи, имеющей передаточную функцию

и состоящую из этого усилительного звена и дифференцирующего контура (рис.4.9, а), необходимо в цепь обратной связи включить интегрирующий контур (рис.4.9, б), передаточная функция которого

При этом для соблюдения эквивалентности цепей необходимо при одной и той же величине ёмкостей активные сопротивления в рассматриваемой схеме выбрать исходя из равенств

Приведённый пример показывает, что инерционная жёсткая связь может быть использована в тех же целях, в каких используется последовательная коррекция дифференцирующим звеном.

Если звено, охватываемое обратной связи, имеет передаточную функцию

то при наличии жёсткой обратной связи следует, что

Это выражение показывает, что применение жёсткой обратной связи к звеньям с астатизмом первого и более высокого порядка приводит к потере астатизма, так как в знаменателе последнего свободный член отличен от нуля.

При большом коэффициенте усиления в прямой цепи вследствие уменьшения коэффициентов характеристического полинома в последней передаточной функции уменьшаются постоянные времени. Например, в случае апериодического звена, охваченного жёсткой обратной связью, когда , имеем

Применение жёсткой обратной связи уменьшает постоянные времени.

Идеальная гибкая жёсткая связь

· не приводит к потере астатизма и превращению астатических звеньев в статические;

· позволяет увеличить демпфирование колебаний;

· в некоторых случаях позволяет уменьшить постоянную времени.

Положительная жёсткая обратная связь применяемая для астатических звеньев даёт неустойчивые звенья, так как свободный член в полиноме знаменателя будет всегда отрицателен.

Для статических звеньев применение положительной жёсткой обратной связи даёт увеличение коэффициента передачи. Например, апериодическое звено, охваченное положительной жёсткой обратной связью, имеет передаточную функцию .

Соответствующим выбором коэффициента можно сделать величину

достаточно малой и тем самым увеличить коэффициент усиления. В этом случае одновременно увеличится и постоянная времени.

Положительные обратные связи по сравнению с отрицательными применяются значительно реже. В основном их используют для увеличения коэффициента усиления усилителей (например, магнитных).

Последовательные и параллельные корректирующие устройства. Динамические свойства САР можно улучшить как последовательными, так и параллельными включениями корректирующих устройств. Во многих случаях задача коррекции решается одновременным применением звеньев последовательного и параллельного включения.

Среди различных по принципу действия корректирующих устройств особенно широко распространены электрические цепи, построенные на элементах активного сопротивления R, ёмкости С и индуктивности L. Последовательные корректирующие звенья, использующие эти элементы, благодаря свой простоте успешно применяются в электрических схемах, где для передачи управляющего сигнала используются модулированные колебания. В последнем случае для коррекции динамических свойств системы применяют либо цепи, которые включаются в канал усиления модулированного сигнала и оказывают непосредственное воздействие на огибающую этого сигнала, либо обычные корректирующие цепи, которые включаются в канал усиления постоянного тока между демодулятором и модулятором.

Для воздействия на огибающую в канале модулированного сигнала применяют звенья только дифференцирующего типа. Среди них следует отметить Т - образный (рис.4.10, а) и двойной Т – образный (рис.4.10, б) контуры, выполняющие операцию дифференцирования огибающей в ограниченном диапазоне частот и вводящие в закон регулирования не только составляющую, пропорциональную входному сигналу, но также и составляющую, пропорциональную производной от огибающей входного сигнала. Характеристики корректирующих устройств переменного тока в сильной степени зависят от изменения несущей частоты, что является существенным недостатком этих цепей постоянного тока, в систему переменного тока включают элементы демодуляции и модуляции для образования части усилительного тракта на постоянном токе.

Зависимость качественных показателей процесса регулирования от нестабильности характеристик элементов системы с применением последовательных корректирующих устройств не уменьшается, что является недостатком последовательной коррекции. Если элементы с передаточной функцией изменяет свои параметры при работе системы, то нестабильность характеристик последовательного соединения корректирующего устройства с указанной группой элементов может быть оценена отношением

Последнее отношение указывает на то, что нестабильность характеристик сказывается прямо пропорционально на выходе устройства с предыдущей передаточной функцией.

Параллельные корректирующие устройства, или отрицательные обратные связи, позволяют уменьшить влияние изменения параметров прямой цепи на выход устройства с параллельной коррекцией. Если элементы охватываются отрицательной обратной связью , что соответствует передаточной функции

то нестабильность характеристик с параллельной коррекцией

Эта формула показывает, что отрицательные обратные связи уменьшают влияние эффекта изменения параметров на протекание процесса регулирования в раз. Отрицательные обратные связи могут успешно применяться для линеаризации тех или иных элементов системы.

Параллельные корректирующие устройства широко используются при охвате исполнительных двигателей отрицательными обратными связями по скорости и ускорению.

В сравнении с последовательными корректирующими устройствами системы с параллельной коррекцией менее подвержены влиянию помех. В качестве параллельных корректирующих устройств могут применяться не только цепи R, C, но и активные четырёхполюсники, в том числе тахогенераторы и дифференцирующие трансформаторы. Параллельные корректирующие устройства во многих случаях имеют более сложную конструкцию, чем последовательные корректирующие устройства.

Понятие об оптимальности переходного процесса. Система, рассчитанная по тому или иному критерию оптимальности, называется оптимальной САР.

Рассмотрим понятие САР оптимальной по времени протекания процесса. В некоторой системе исполнительный двигатель обеспечивает максимально возможное ускорение, которое не превышает величину : .

Переходный процесс в этой системе, вызванный ступенчатым воздействием , протекает в течение времени и показан на рис.3.75, а в виде кривой0АВ.

Пусть скорость изменения выходной величины равна . Легко заметить, что значение выходной величины после окончания переходного процесса определяется площадью под кривой ,так как =

и . Требуется выбрать такой закон регулирования, чтобы при заданном выше ограничении обеспечить минимум времени регулирования .Иначе говоря, необходимо выбрать такой закон изменения скорости , чтобы при заданной площади под кривой и при ограничении время было минимальным.

Основываясь на принципе максимума, сформулированном Л.С. Понтрягигиным, можно показать, что закон изменения скорости должен соответствовать равнобедренному треугольнику (рис.4.11, б), у которого наклон сторон определяется максимально возможным ускорением. Это означает, что в течении первой половины времени переходного процесса (участок 0А, рис.4.11, а) система разгоняется с постоянным максимальным ускорением (рис.4.11, в). Во второй половине переходного процесса (участок АВ) система тормозится с тем же предельным значением отрицательного ускорения. Подобный режим требует осуществления релейного закона управления.

Если минимальное время переходного процесса обозначить через , то для периода разгона можно написать . Следовательно, минимальное время переходного процесса . Представляя переходный процесс 0АВ в виде суммы трёх парабол:

В.В.Солодовников показал, что передаточная функция разомкнутой оптимальной по быстродействию системы

Эта передаточная функция является трансцендентной функцией переменной и может быть реализована с помощью линейных систем только лишь приближённо. Логарифмическая АЧХ, соответствующая этой передаточной функции, имеет частоту среза и наклон в области частот, близких частоте среза, приблизительно равный -20 дБ/дек.

В случае астатических систем когда частота среза равна . Эта формула указывает на то, что частота среза или полоса пропускания в оптимальной системе определяется максимально возможным ускорением, которое способен обеспечить исполнительный двигатель. Полоса пропускания в реальной системе при заданных ограничениях на ускорение не может быть более широкой, чем та, которая устанавливается последним выражением.

Связь частоты среза с оценками качества переходного процесса. Процесс построения желаемых частотных характеристик в значительной степени упрощается, если существуют зависимости, устанавливающие связь между основными параметрами частотных характеристик, с одной стороны, и показателями качества процесса регулирования – с другой. Поэтому, прежде чем сформулировать основные положения по построению желаемых характеристик, рассмотрим связь частоты среза, приближённо характеризующую полосу пропускания системы, с такими оценками качества переходного процесса, как время регулирования и перерегулирование.

В простейшем случае вещественная частотная характеристика замкнутой системы может быть аппроксимирована одной трапецией с коэффициентом наклона (пмс.4.12, а). Обычно интервал, соответствующий частоте называют интервалом положительности. Изменяя коэффициент наклона трапеции в пределах и пользуясь таблицами h-функций, можно построить семейство переходных процессов и по нему определить зависимость времени регулирования и перерегулирования от коэффициента . Каждая из кривых семейства, соответствующая определённому коэффициента наклона трапеции будет характеризоваться уравнением .

Так как , то, вводя в рассмотрение относительное время и считая, что время переходного процесса определяется моментом вхождения процесса в пятипроцентную трубку , можно получить графики и , показанные на рис.3.74, б, в.

Из рис.4.12, б следует, что время переходного процесса при изменении коэффициента от 0 до 1 находится в пределах .

Нижний предел соответствует коэффициент =0,2-0,25, а верхний предел - коэффициенту =0 и =1.

Рис.4.12, в показывает, что перерегулирование возрастает при .

Частота среза и интервал положительности связаны соотношением , где коэффициент и зависит от высоты и коэффициента наклона трапеции. Вводя последе выражение в предпоследнее, легко получить верхнюю и нижнюю границы времени переходного процесса, выраженные через частоту среза.

Чаще встречается вещественная характеристика, представленная на рис.4.13, а и аппроксимируемая двумя трапециями. Одна из трапеций имеет высоту и коэффициент наклона . Вторая трапеция обладает высотой и коэффициентом наклона . Для более полного описания вещественной характеристики обычно в рассмотрение вводят ещё коэффициент формы . Связь между частотой среза и оценки качества переходного процесса можно установить следующим образом.

На основании рис.4.13, а легко определить

Переходная функция, отвечающая рассматриваемой вещественной характеристике описывается уравнением

или , то при значение . Следовательно, .

Вводя в рассмотрение относительное время и вычисляя переходные процессы для различных коэффициентов и , можно определить максимально возможные перерегулирование и время переходного процесса при заданном значении . Повторяя вычисления при иных заданных значениях , получим возможность построить кривые и . В.В. Солодовниковым для случая (рис.4.13, б, в) и для случая, когда

Рис.4.13, б, в позволяют при заданных значениях и определить максимально возможные величины и . Если задаются перерегулирование и время переходного процесса , то, определив величину (рис.4.13, б), можно установить сначала значение ординаты (рис.4.13, в), которая должна соответствовать найденной величины и быть равной заданному значению , а затем вычислить частоту среза: .

Если на вещественной характеристике существует отрицательный экстремум (рис.4.14), то вызванное им дополнительное перерегулирование можно оценить неравенством или .

Результирующее перерегулирование, обусловленное наличием положительного и отрицательного экстремумов на вещественной характеристике, определяется соотношением .

Пусть, например, необходимо, чтобы перерегулирование не превышало 32%. Если при этом Р_max=1,2, то согласно графику (см. рис.4.13, б) . Для соблюдения последнего неравенства нужно выбрать = - 0,2. В этом случае что соответствует .

Выполнение этого условия означает, что АФХ разомкнутой системы, построенная в координатах номограммы, предназначенной для построения , не должна заходить внутрь области, которая ограничена кривыми с индексами и . Приближённо эта область на рис.4.7 отмечена штриховым прямоугольником. Последнее условие эквивалентно обеспечению определённого запаса устойчивости по модулю и фазе. Для проведённого примера запас устойчивости по модулю приблизительно равен + 16 дБ и определяется половиной стороны (2L) указанного прямоугольника, приведённой параллельно оси ординат. Запас устойчивости по фазе равен + 45^о и находится по второй стороне (2γ) прямоугольника, параллельной оси абсцисс.

Таким образом, для того чтобы перерегулирование не превосходило заданной величины σ при соответствующих значениях и , необходимо в том диапазоне частот, где ЛАЧХ удовлетворяет условию

, иметь избыток фазы в системе не меньше величины γ.

Анализ построенных переходных процессов, соответствующих вещественной характеристике (рис.4.14) при различных её параметрах и при одном и том значении , показал, что время регулирования практически (например, при ) не зависит от формы вещественной характеристики в интервале частот .

Построение желаемой ЛАЧХ в соответствии с требованиями, предъявляемыми к качеству. Желаемые ЛЧХ, обеспечивающие заданные показатели качества регулирования построить различными способами: по заданным коэффициентам ошибок и запасу устойчивости по фазе; по заданным показателю колебательности и порядку астатизма; по заданным значениям перерегулирования, времени переходного процесса и ускорения.

Рассмотрим последний вариант построения желаемой ЛАЧХ , когда в переходном процессе, вызванном ступенчатым управляющим сигналом, требуется обеспечить перерегулирование и время регулирования, не превосходящие и . Максимально возможное ускорение координаты заодно; предполагаются также заданными порядок астатизма и передаточный коэффициент .

Рис.4.15. Построение желаемой ЛАЧХ

Процесс построения желаемой ЛАХ разбивается на четыре этапа: построение в области низких частот, построение в интервале средних частот, построение в высокочастотной области и осуществление сопряжения построенных участков характеристики.

В области низких частот форма ЛАЧХ определяется порядком астатизма и передаточным коэффициентом . При этом желаемая ЛАХ представляется прямой, соответствующей уравнению .

Эта низкочастотная асимптота имеет наклон -.20 дБ/дек и пересекается с осью нулевого усиления при . Ордината прямой при равна . Следовательно, для построения низкочастотной асимптоты желаемой ЛАХ (рис.4.15, а) нужно через точку или провести прямую с наклоном - .20 дБ/дек. Ордината АС определяет коэффициент усиления в синтезируемой системе регулирования.

В интервале средних частот желаемая ЛАХ определяется заданными значениями перерегулирования и времени переходного процесса . Из соображений приближения реального процесса к оптимальному наклон среднечастотной асимптоты желаемой ЛАХ берут равным – 20 дБ/дек. Выбор частоты среза осуществляют на основании неравенства .

С одной стороны, частота среза проектируемой системы должна быть меньше частоты среза оптимальной системы, вычисляемой по заданным значениям ускорения и управляющего сигнала . С другой стороны, частота среза с целью обеспечения времени переходного процесса, не превышающего заданной величины , не должна быть меньше частоты , которая находится на основании рис.4.15, б, в в соответствии с заданными значениями и . Длина среднечастотной асимптоты или интервал частот, который она охватывает, должны быть выбраны по определённым из рис.4.15, б, в значениям и . Величины и позволяют по номограмме (см. рис.3.48) установить запретную область, куда не должна заходить желаемая АФХ. Если стороны прямоугольника, характеризующего запретную область, равны 2L и 2γ, то в диапазоне частот (рис.4.15, б), где желаемая ЛАХ удовлетворяет неравенству , фазовая характеристика должна иметь избыток фазы не меньше γ. Обычно среднечастотная асимптота охватывает интервал частот не меньше декады.

В области высоких частот форма желаемой ЛАХ принимается такой же, как и форма неизменяемой ЛАХ, построенной с учётом заданных значений порядка астатизма и добротности К. Область высоких частот оказывает малое влияние на качество переходного процесса и определяет лишь начальную часть процесса регулирования.

Сопряжение низкочастотной и среднечастотной асимптот желаемой ЛАХ, а также среднечастотной части желаемой характеристики с высокочастотным участком производится с помощью прямых, наклон которых не должен отличаться от наклона соседних асимптот более чем на -20 или – 40 дБ/дек. Использование сопрягающих асимптот с большим наклоном приводит в получении нужных значений запаса устойчивости по модулю и по фазе. Сопряжение должно осуществляться так, чтобы в интервале частот, где выполняется последнее неравенство, избыток был не меньше γ.

Избыток фазы на левой стороне среднечастотной асимптоты

где - сопрягающие частоты; они меньше частоты 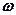, при которой вычисляется 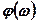; - число сопрягающих частот, при которых наклон асимптот изменяется на +20 дБ/дек.

Для определения избытка фазы на правой стороне среднечастотной асимптоты применяют приближённое выражение

где сопрягающие частоты, расположенные правее граничной частоты в точке (рис.4.15, б); - сопрягающие частоты, расположенные между частотой среза и граничной частотой в точке ; - относительный наклон желаемой ЛАХ в интервале средних частот (при наклоне -20 дБ/дек ).

Пример. Передаточная функция неизменяемой части , где .

Указанные значения для астатизма и передаточного коэффициента необходимо реализовать в скорректированной системе, которая не должна иметь перерегулирование, превышающее , и время переходного процесса, превышающее . Максимально возможное ускорение в системе определяется величиной w_m=40 рад/с² при начальном рассогласовании

Процесс построения желаемой ЛАХ имеет следующие этапы.

В соответствии с передаточной функцией строится ЛАХ неизменяемой части системы

Низкочастотная асимптота АВ построенной характеристики (рис.4.16) является желаемой ЛАХ в области низких частот и определяется уравнением при .

Рис.4.16. Пример построения желаемой ЛАЧХ

Частота среза для оптимального процесса