Теорема Калмана в задачи оптимальной стабилизации

Классификация задач оптимального управления

1. По виду ограничений (ограничение имеет вид равенства)
; .

2. Ограничение типа неравенства
; .

3. По виду краевых условий
– начальное состояние системы;
– конечное состояние системы;
Если они зафиксированы, то говорят о задаче управления с фиксированными концами.
Если , то задача оптимального управления с подвижными концами.

4. По времени начала и окончания процесса

5. По критерию оптимальности или по виду целевой функции (функционала)

5.1. Функционал в виде Больца

5.2. Функционал в виде Лагранжа

5.3. Функционал в виде Майера

Если производительность объекта в единицу времени, то функционал определяет производительность реактора на всем интервале функционирования. Или если – энергетические затраты, связанные с реализацией управления 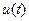в единицу времени, то – это энергетические затраты на временном интервале, например, на режиме стабилизации.

Задача построения оптимального регулятора с помощью отрицательной обратной связи (методом Калмана)

– квадратичный функционал потерь

;

;
;

, где

– желаемое значение;

– коэффициент значимости (важности) веса -ой компоненты вектора состояния, которое определяется как отношение:

, где

– максимально допустимое значение ошибки управления по -ой компоненте. Чем больше допустимое значение, тем меньше вес (значение)

– мера отклонения от заданного значения на интервале по -ой компоненте вектора состояния.

– коэффициент важности (значимости) -ой компоненты вектора управления;

– максимально допустимое значение -ой компоненты.

‚ – энергетические затраты по -ой компоненте вектора управления на интервале .

– суммарные энергетические затраты связанные при управлении .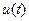

В соответствии с этим функционалом мера отклонения траектории (ошибка управления) определяется составляющей

Задача оптимального управления состоит в том, чтобы выбрать оптимальное управление 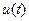, путем построения регулятора при минимизации погрешности управления энергетических затрат на это управление.

– диагональная матрица

Ограничения для этой задачи:

;
;
.

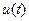выбрать таким образом, чтобы функционал

– определяет степень отклонения, ошибку управления, норма отклонения от желаемой траектории движения;

– энергетические затраты, связанные с выбранной задачей реализацией заданной траектории.

Связан с выбором оптимизирующей отрицательной обратной связи.

;

– непрерывная функция времени

– кусочно-непрерывная функция

Особенностью задачи оптимальной стабилизации ООС является возможность определить матрицу , дающую наилучший результат в смысле критерия при любых начальных условиях. Этому утверждению соответствует теорема: пусть существует положительная определенная матрица , которая является решением матричного квадратичного уравнения:

– уравнение Риккати-Лурье

и матрица , связанная с соотношением:

тогда при любых начальных условиях оптимальная стабилизация обеспечивается управлением:

причем линейное значение показателя качества – функционал определяется:

Для существования единственности положительного решения матричного квадратного уравнения достаточно, чтобы

пара матриц была невырожденной;
матрица должна быть положительно определенной;
матрица должна быть неотрицательно определенной и при этом должна быть также невырожденной.

Матрица является матрицей симметричной

, где

(должен быть не меньше заданного запаса устойчивости)