Точечные оценки параматров распределения

 

Мы подошли к решению вопроса о том, как на основании полученной в эксперименте группы результатов наблюдений оценить истинное значение, т.е. найти результат измерений, как оценить его точность, т.е. меру его приближения к истинному значению.

Рассмотренные в рамках предыдущей лекции функции распределения описывают пове­дение непрерывных случайных величин, т.е. величин, возможные значения которых неотделимы друг от друга и непрерывно запол­няют некоторый конечный или бесконечный интервал. На прак­тике все результаты измерений и случайные погрешности являют­ся величинами дискретными, т.е. величинами x_i возможные зна­чения которых отделимы друг от друга и поддаются счету. При использовании дискретных случайных величин возникает задача нахождения точечных оценок параметров их функций распределе­ния на основании выборок – ряда значений х_i принимаемых слу­чайной величиной х в n независимых опытах. Используемая вы­борка должна быть репрезентативной(представительной), т.е. должна достаточно хорошо представлять пропорции генеральной совокупности.

Оценка параметра называется точечной, если она выражается одним числом. Задача нахождения точечных оценок – частный случай статистической задачи нахождения оценок параметров функции распределения случайной величины на основании выбор­ки. Любая точечная оценка, вычисленная на основании опытных данных, является их функцией и поэтому сама должна представлять собой случайную величину с распределением, зависящим от распределения исходной случайной величины, в том числе от самого оцениваемого параметра и от числа опытов n.

Точечные оценки могут быть состоятельными, несмещенными и эффективными.

Состоятельной называется оценка, которая при увеличении объема выборки стремится по вероятности к ис­тинному значению числовой характеристики.

Несмещеннойна­зывается оценка, математическое ожидание которой равно оце­ниваемой числовой характеристике (параметру).

Оценка называется эффективной, если ее дисперсия меньше дисперсии любой другой оценки данного параметра, т.е. наиболее эффективной счи­тают ту из нескольких возможных несмещенных оценок, которая имеет наименьшую дисперсию.

Требование несмещенности на прак­тике не всегда целесообразно, так как оценка с небольшим сме­щением и малой дисперсией может оказаться предпочтительнее несмещенной оценки с большой дисперсией. На практике не все­гда удается удовлетворить одновременно все три этих требова­ния, однако выбору оценки должен предшествовать ее критиче­ский анализ со всех перечисленных точек зрения.

Наиболее распространенным методом получения оценок явля­ется, метод наибольшего (максимального) правдоподобия, теоретически обоснованный математиком Р. Фишером, который приводит к асимптотически несмещенным и эффективным оценкам с при­ближенно нормальным распределением. Среди других методов мож­но назвать методы моментов и наименьших квадратов.

Точечной оценкой математического ожидания результата измерений является среднее арифметическое значение измеряемой величины

(6.1)

При любом законе распределения оно является состоятельной и несмещенной оценкой, а также наиболее эффективной по крите­рию наименьших квадратов.

Точечная оценка дисперсии, определяемая по формуле

(6.2)

является несмещенной и состоятельной.

Среднеквадратическое отклонение случайной величины х определяется как корень квадрат­ный из дисперсии. Соответственно его оценка может быть найдена путем извлечения корня из оценки дисперсии. Однако эта опера­ция является нелинейной процедурой, приводящей к смещенности получаемой таким образом оценки. Для исправления оценки СКО вводят поправочный множитель k(n), зависящий от числа наблю­дений n. Он изменяется от k(3)=1,13 до k(∞) = 1,03. Оценка сред­него квадратического отклонения

Полученные оценки математического ожидания и СКО являются случайными величи­нами. Это проявляется в том, что при повторениях серий из n наблюдений каждый раз будут получаться различные оценки и 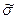. Рассеяние этих оценок целесообразно оценивать с помощью СКО 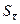и S_σ. Оценка СКО среднего арифметического значения

(6.3)

Оценка СКО среднего квадратического отклонения

Отсюда следует, что относительная погрешность определения СКО может быть оценена как

Она зависит только от эксцесса и числа наблюдений в выборке и не зависит от СКО, т.е. той точности, с которой производятся измерения. Ввиду того, что большое число измерений проводит­ся относительно редко, погрешность определения, а может быть весьма существенной. В любом случае она больше погрешности из-за смещенности оценки, обусловленной извлечением квадрат­ного корня и устраняемой поправочным множителем k(n). В связи с этим на практике пренебрегают учетом смещенности оценки СКО отдельных наблюдений и определяют его по формуле

(6.4)

т.е. считают k(n)=1.

Иногда оказывается удобнее использовать следующие формулы для расчета оценок СКО отдельных наблюдений и результата измерения:

; (6.5)

Точечные оценки других параметров распределений использу­ются значительно реже. Оценки коэффициента асимметрии и экс­цесса находятся по формулам

; (6.6)

(6.7)

Определение рассеяния оценок коэффициента асимметрии и экс­цесса описывается различными формулами в зависимости от вида распределения.