На движущийся электрический заряд. Сила Лоренца
Действие магнитного поля
Сила, действующая, согласно закону Ампера, на проводник с током в магнитном поле, есть результат его воздействия на движущиеся электрические заряды, создающие этот ток.
Рассмотрим цилиндрический проводник длиной l стоком I, расположенный в магнитном поле индукции 
(рис. 13.8). Скорость направленного движения некоторого положительного заряда q равна u. Сила, действующая на отдельный движущийся заряд, определяется отношением силы F, приложенной к проводнику с током, к общему числу .N этих зарядов в нем:
(13.17)
Рис. 13.8
Раскроем выражение для силы, используя (13.13) и полагая, что сила тока равна
где j — плотность тока. Учитывая (12.50), получаем
(13.18)
где п = N/(Sl) — концентрация частиц. Подставляя (13.18) в (13.17), получаемвыражение для силы, действующей со стороны магнитного поля на отдельный движущийся электрический заряд и называемой силой Лоренца:
Направление силы Лоренца можно определить из векторной записи уравнения (13.19) с учетом знака заряда q:
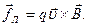(13.20)
Как видно из (13.20), эта сила всегда перпендикулярна плоскости, в которой лежат векторы 
и . Из механики известно, что если сила перпендикулярна скорости, то она изменяет лишь ее направление, но не значение. Следовательно, сила Лоренца не изменяет кинетической энергии движущегося заряда и не совершает работы.
Если заряд неподвижен относительно магнитного поля или его скорость параллельна (антипараллельна) вектору магнитной индукции, то сила Лоренца равна нулю.
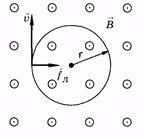Пусть в однородное магнитное поле перпендикулярно вектору индукции влетает со скоростью v положительно заряженная частица (рис. 13.9). На нее действует сила Лоренца fЛ, которая вызовет центростремительное ускорение, и, по второму закону Ньютона,
mu2/r=quB, (13.21)
где q и т — заряд и масса частицы, r — радиус траектории, по которой она будет двигаться. Из (13.21) получаем
Рис. 13.9 r = mu/(qB). (13.22)
Отсюда следует, что радиус траектории остается постоянным, а сама траектория есть окружность.
Используя (13.22) и считая, что значение скорости частицы не изменяется, найдем период вращения ее по окружности:
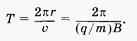(13.23)
Отношение q/m называют удельным зарядом частицы. Период вращения ее в магнитном поле [см. (13.23)] не зависит от радиуса окружности и скорости, а определяется только магнитной индукцией и удельным зарядом. Эту особенность используют в ускорителе заряженных частиц — циклотроне.
Чтобы описать форму траектории заряженной частицы, влетающей со скоростью в однородное магнитное поле под произвольным углом к (рис. 13.10), разложим вектор и на две составляющие и 
|| и ^, направленные соответственно вдоль вектора магнитной индукции магнитного поля и перпендикулярно ему. Составляющая || при движении частицы в магнитном поле остается постоянной; сила Лоренца, действующая на частицу, изменит направление составляющей скорости ^. Под действием этой силы частица вращается по окружности. Таким образом, траекторией движения будет винтовая линия — вращение по окружности со скоростью ^ совместно с перемещением вдоль вектора магнитной индукции со скоростью ||.
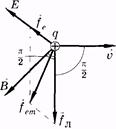
Если на движущуюся заряженную частицу q действуют электрическое поле с напряженностью 
и магнитное поле с магнитной индукцией (рис. 13.11), то результирующая сила равна
(13.24)
Во многих системах (осциллограф, телевизор, электронный микроскоп) осуществляют управление электронами или другими заряженными частицами, воздействуя на них электрическими и магнитными полями, в этом случае основной расчетной формулой является (13.24).