Выпуклость графика функции. Точки перегиба

График дифференцируемой функции у = f(x)называется выпуклым внизна интервале (a; b), если он расположен выше любой ее касатель­ной на этом интервале. График функции у = f(x) называется выпуклым вверхна интервале (a; b), если он расположен ниже любой ее касательной на этом интервале.

Точка графика непрерывной функции у = f(x),отделяющая его части разной вы­пуклости, называется точкой перегиба.

На рисунке 14 кривая у = f(x)выпу­кла вверх в интервале (a; c), выпукла вниз в интервале (с; b), точка М(с; f(с)) — точка перегиба.

Рис. 14.

Теорема.Если функция у = f(x) во всех точках интервала

(a; b) имеет от­рицательную вторую производную, т. е. f "(x) <0, то график функции в этом ин­тервале выпуклый вверх. Если же f "(x) > 0 x 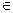(a; b)— график выпуклый вниз.

Теорема (достаточное условие существования точек перегиба).Если вторая производная f "(x) при переходе через точку x₀, в которой она равна ну­лю или не существует, меняет знак, то точка графика с абсциссой x₀ есть точка перегиба.