НЕПРЕРЫВНОСТЬ ФУНКЦИИ

5.1. Непрерывность функции в точке

Пусть функция у = f(x)определена в точке x₀и в некоторой окрест­ности этой точки.

Определение 1. Функция у = f(x)называется непрерывной в точке x₀, если существует предел функции в этой точке и он равен значению функ­ции в этой точке, т. е.

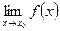= f(x₀) (6.1)

Определение 2. Функция у = f(x)называется непрерывной в точке x₀, если для любой последовательности {x_n} точек из области определения функции сходящаяся к точке x₀, соответствующая последовательность {f(x_n)} значений функции f(x) сходится к f(x₀).

Равенство (6.1) означает выполнение трех условий:

1) функция f(x)определена в точке x₀и в ее окрестности;

2) функция f(x)имеет предел при х → x₀;

3) предел функции в точке x₀равен значению функции в этой точке, т. е. выполняется равенство (6.1).

Так как , то равенство (6.1) можно записать в виде

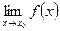== f(x₀) (6.2)

Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции,то есть в функцию f(x)вместо аргумента х подставить его предельное значение x₀.

Пример. Вычислить А = .