Вычисление пределов

Первым замечательным пределом

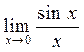= 1.

Для раскрытия неопределённостей вида 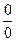часто бывают полезным

применять принцип замены бесконечно малых эквивалентными и дру­гие свойства эквивалентных бесконечно малых функций. Как известно, sin x ~ х при х →0, tg x ~ х при x → 0. Приведем еще примеры эквива­лентных б. м. ф.

Ниже приведены важнейшие эквивалентности,которые используют­ся при вычислении пределов:

 

1. sin х ~ х при х → 0; 6. е^х -1~ х (х → 0);

2. tg x ~ х (х → 0); 7. а^х - 1 ~ x·lnа (x → 0);

3. arcsin x ~ х (х →0); 8. ln(1 + х)~ x (х → 0);

4. arctg x ~ x (x → 0); 9. log_a(l + х)~ х·log_a е (x → 0);

5. 1 – cos x ~ 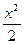(x → 0); 10. (1 + x)^k - 1 ~ k · х, k > 0 (х → 0);

в частности, ~.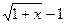

 

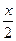Пример. Найти .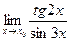

Решение: Так как tg 2х ~ 2x, sin 3х ~ 3x; при x → 0, то

.

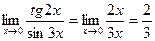Второй замечательный предел.

(5.2)