Основные теоремы о пределах

Рассмотрим теоремы, которые облегчают нахождение пределов функции. Формулировка и доказательство теорем для случаев, когда x → x₀ и x → ∞, аналогичны. В приводимых теоремах будем считать, что пределы 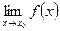,существуют.

Теорема 1.Предел суммы (разности) двух функций равен сумме (разности) их пределов:

.

Теорема 2.Предел произведения двух функций равен произведению их пределов:

.

Следствие.Постоянный множитель можно выносить за знак предела:

.

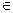Следствие.Предел степени с натуральным показателем равен той же степени предела: Вчастности, , n N.

Теорема 3.Предел дроби равен пределу числителя, деленному на предел зна­менателя, если предел знаменателя не равен нулю:

()