Односторонние пределы

Число А₁ называется пределом функции у = f(x) слевав точке x₀, если для любого число ε> 0 существует число δ = δ(ε)> 0 такое, что при х 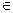(x₀ - δ; x₀), выполняется неравенство |f (x) — А| < ε. Предел слева записывают так: 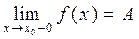или коротко: f(x₀ - 0) = A (см. рис. 2).

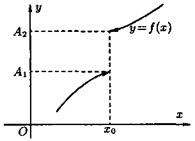
Рис. 2.

Аналогично определяется предел функции справа,запишем его с по­мощью символов:

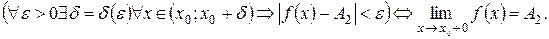
Коротко предел справа обозначают f(x₀ + 0) = A₂.

Пределы функции слева и справа называются одностороннимипре­делами. Очевидно, если существует, ,то существуют и оба односторонних предела, причем A=A₁=A₂.

Справедливо и обратное утверждение: если существуют оба предела

f(x₀-0) и f(x₀+ 0) и они равны, то существует предел А = 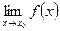и А = f(x₀-0). Если же A₁ ≠ A₂,то 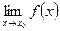не существует.

 

3.3. Предел функции при x →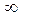

Пусть функция у = f(x)определена в промежутке (-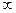;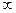). Определение. Число А называется пределом функцииf(x)при х → 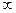, если для любого положительного числа ε существует такое число М = М(ε) > 0, что при всех х,удовлетворяющих неравенству |х| > М выполняется неравенство

|f(x) — А|<ε. Коротко это определение можно записать так:

Если х → +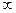, то пишут A= , если x → -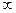, то - А=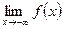

Геометрический смысл этого определения таков: для 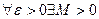, что при

х 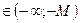или x 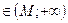соответствующие значения функции f(x) попадают в ε-окрестность точки А,т. е. точки графика лежат в полосе шириной 2ε, ограниченной прямыми у= А + ε и y= А -ε (см. рис. 3).

 

Рис. 3.

Определение. Число A называется пределом функции при x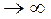, если для любой последовательности {x_n} значение x из области определение f(x) такой, что x_n 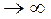, соответсвующая последовательность {f(x­_n)} значений функции f(x) сходится и притом всегда к одному и тому же числу A.