Помилки вибірки і теоретичні основи вибіркового методу.
Для того, щоб мати підстави поширити результати вибіркового спостереження на генеральну сукупність, необхідно знати наскільки добре вибіркова сукупність представляє генеральну. Тобто, чи репрезентативна вибірка.
Вибірка, як уже відзначалося, вважається репрезентативною, якщо узагальнюючі показники вибіркової і генеральної сукупності досить близькі.
Звичайно порівнюють такі показники вибіркової і генеральної сукупності:
– середню величину тієї чи іншої ознаки в одиниць сукупності (середня зарплата, середній доход, середня врожайність);
– частку одиниць, що мають ту чи іншу ознаку, тобто питому вагу певних одиниць у сукупності (частка осіб з вищою освітою, частка жінок у загальній чисельності працівників і т.ін.).
Різниця між цими показниками вибіркової і генеральної сукупності і називається помилкою репрезентативності, тобто:
 , помилка репрезентативності середньої величини,
, помилка репрезентативності середньої величини,
 , помилка репрезентативності для частки.
, помилка репрезентативності для частки.
Вибіркова середня і частка є змінними величинами, тому що вони можуть приймати різні значення у залежності від того, які одиниці генеральної сукупності потрапили у вибірку.
Тобто з однієї і тієї ж генеральної сукупності можна зробити ряд вибірок рівного обсягу. При цьому кожна вибірка буде мати свою помилку репрезентативності для середньої і для частки.
Тому з усіх можливих помилок репрезентативності визначається середня помилка вибірки, що позначається буквою m. Її ще називають стандартна помилка.
Перш ніж записати формули, за допомогою яких визначаються середні помилки вибірки, розглянемо від чого залежить величина цих помилок.
Зрозуміло, що чим більше одиниць відбирається з генеральної сукупності, тим ближче вибіркові показники (середня і частка) наближаються до генеральних.
А якщо чисельність вибірки (n) досягне чисельності генеральної сукупності (N), тобто коли вибіркове спостереження перетвориться у суцільне, те взагалі ніяких розбіжностей між вибірковими і генеральними показниками не буде, а помилка вибірки буде дорівнює нулю. Отже:
1.помилка вибірки залежить від обсягу (чисельності) вибірки – обернено пропорційна чисельності вибірки;
2.помилка вибірки залежить від коливання (варіювання) значень ознаки у генеральній сукупності – прямо пропорційна коливанням значень ознаки у генеральній сукупності;
3.від способу відбору одиниць з генеральної сукупності.
Ступінь коливань значень ознаки у сукупності визначається, як відомо, показниками варіації. Основними з них є дисперсія  і СКВ
і СКВ  .
.
З групи теорем Закону великих чисел випливає:
– при власне-випадковому відборі, організованому за схемою повторної вибірки, між помилкою вибірки (m), дисперсією  і чисельністю вибірки (n) існує залежність:
і чисельністю вибірки (n) існує залежність:
 .
.
Тобто середня помилка вибірки являє собою СКВ вибіркової середньої від генеральної. Вона дорівнює кореню квадратному з відношення дисперсії ознаки у генеральній сукупності до числа одиниць вибіркової сукупності.
Але в зв’язку з тим, що практично дисперсія ознаки у генеральній сукупності невідома, то у приведеній формулі використовують дисперсію чи СКВ вибіркової сукупності.
Це обґрунтовано тим, що при дотриманні принципу випадковості відбору одиниць з генеральної сукупності дисперсія достатньої за обсягом вибірки прагне відобразити дисперсію в генеральній сукупності. При цьому вона менша генеральної на величину  (
( ) (якщо n досить велике, те це відношення близьке до одиниці).
) (якщо n досить велике, те це відношення близьке до одиниці).
У випадку малої вибірки, тобто коли чисельність її менше 30 одиниць, у знаменнику формули замість (n) береться (n-1), тобто
 .
.
Якщо вибіркове спостереження застосовується для визначення частки якої-небудь ознаки у сукупності, то середня помилка вибіркової частки обчислюється за формулою:
 ,
,
де  – частка одиниць, що мають певну ознаку у вибірці;
– частка одиниць, що мають певну ознаку у вибірці;
 – частка одиниць які не мають цієї ознаки;
– частка одиниць які не мають цієї ознаки;
 – кількість одиниць вибірки;
– кількість одиниць вибірки;
 – дисперсія частки ознаки у вибірковій сукупності.
– дисперсія частки ознаки у вибірковій сукупності.
При власне-випадковому відборі, організованому за схемою безповторної вибірки, чисельність одиниць генеральної сукупності в процесі відбору скорочується.
Тому при безповторному відборі у наведені формули вводиться додатковий множник:
 ,
,
де  – кількість відібраних одиниць;
– кількість відібраних одиниць;
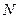 – кількість одиниць генеральної сукупності;
– кількість одиниць генеральної сукупності;
 – частка відібраних одиниць з генеральної сукупності;
– частка відібраних одиниць з генеральної сукупності;
 – частка невідібраних (що залишилися) одиниць генеральної сукупності.
– частка невідібраних (що залишилися) одиниць генеральної сукупності.
Тоді середня помилка вибіркової середньої при безповторному відборі дорівнює:
 ,
,
а середня помилка частки:
 .
.
Так як  завжди менше
завжди менше 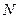 , те множник (
, те множник ( ) завжди менший одиниці. Тому величина середньої помилки вибірки при безповторному відборі менша, ніж при повторному, тому що підкореневе значення формули збільшується на число, менше одиниці.
) завжди менший одиниці. Тому величина середньої помилки вибірки при безповторному відборі менша, ніж при повторному, тому що підкореневе значення формули збільшується на число, менше одиниці.
При порівняно невеликій частці відібраних одиниць, даний множник буде близький до одиниці і ним можна знехтувати.
На практиці часто при визначенні середньої помилки вибірки використовують формули без цього множника, хоча вибірка й організована як безповторна.
Величина помилки вибірки при цьому трохи збільшується.
Наведені формули дають можливість визначити величину середнього відхилення вибіркової середньоївід генеральної, чи вибіркової частки ознаки від генеральної частки.
Разом з тим, при вирішенні практичних задач однієї тільки середньої помилки вибірки недостатньо.
Це пов'язано з тим, що при визначенні помилки конкретної вибірки фактична помилка може бути більша чи менша середньої (m). Тому на практиці користаються звичайно не середньою, а граничною помилкою вибірки, тобто межами, за які не вийде фактична помилка вибірки. Вона дозволяє установити в яких межах знаходиться величина генеральної середньої.
Гранична помилка вибірки  , крім всього іншого, залежить ще і від того, з якою імовірністю вона гарантується.
, крім всього іншого, залежить ще і від того, з якою імовірністю вона гарантується.
На величину імовірності вказує коефіцієнт довіри  , що визначається на основі теорем П.Л. Чебышева й А.М. Ляпунова і інтеграла Лапласа:
, що визначається на основі теорем П.Л. Чебышева й А.М. Ляпунова і інтеграла Лапласа:
 ,
,
де  .
.
Ці теореми визначають імовірність того, що гранична помилка вибірки  не перевищить
не перевищить  -кратну (узяту
-кратну (узяту  раз) середню помилку вибірки (m).
раз) середню помилку вибірки (m).
Таким чином,  указує на імовірність розбіжності
указує на імовірність розбіжності  , тобто на імовірність того, на яку величину генеральна середня буде відрізнятися від вибіркової середньої.
, тобто на імовірність того, на яку величину генеральна середня буде відрізнятися від вибіркової середньої.
Так, з імовірністю  можна гарантувати, що різниця між вибірковою і генеральної середньою не перевищить величини однократної середньої помилки вибірки.
можна гарантувати, що різниця між вибірковою і генеральної середньою не перевищить величини однократної середньої помилки вибірки.
З імовірністю  можна гарантувати, що розмір граничної помилки не перевищить дворазової середньої помилки (при
можна гарантувати, що розмір граничної помилки не перевищить дворазової середньої помилки (при  =2).
=2).
З імовірністю  – не перевищить 3-х кратної середньої помилки (при
– не перевищить 3-х кратної середньої помилки (при  =3).
=3).
Це так називане «правило трьох сігм». Відповідно до цього правила величину граничної помилки вибірки обчислюють з деякою імовірністю ( ), якій відповідає
), якій відповідає  -кратне значення (m).
-кратне значення (m).
Величина імовірності для різних значень коефіцієнта ( ) приводиться в спеціально розрахованих таблицях, що приводяться у курсі математичної статистики.
) приводиться в спеціально розрахованих таблицях, що приводяться у курсі математичної статистики.
Рекомендується запам'ятати наступні значення відповідних одне одному  і
і  , розраховані за формулою:
, розраховані за формулою:
 – інтеграл Лапласа,
– інтеграл Лапласа,
де  .
.

| 
|
| 0,683 | |
| 0,954 | |
| 0,997 | |
| 0,999 |
Таким чином гранична помилка вибірки залежить від трьох факторів:
– обсягу вибірки,  ;
;
– ступеня коливань значень ознаки  ;
;
– необхідної гарантованої імовірності (коефіцієнта довіри,  ).
).
З введенням коефіцієнта кратності помилки формула граничної помилки має вигляд:
 .
.
Підставивши в цю формулу замість (m) її аналітичне значення одержимо загальні формули граничної помилки.
1.При повторному власне-випадковому відборі:
– для середньої величини ознаки:  ;
;
– для частки:  .
.
2.При безповторном у власне-випадковому і механічному:
– для середньої:  ;
;
– для частки:  .
.
3.При типовому відборі дисперсією ознаки є середня з групових дисперсій:
 ,
,
де  – вибіркова дисперсія в i-тій типовій групі, вона визначається за формулою:
– вибіркова дисперсія в i-тій типовій групі, вона визначається за формулою:  ;
;
 – число одиниць у i-й типовій групі.
– число одиниць у i-й типовій групі.
Для частки середня з групових дисперсій визначається:
 .
.
Тоді гранична помилка вибіркової середньої при типовому повторному відборі буде дорівнює:
 ;
;
частки:  .
.
4.При типовому безповторном відборі:
для середньої:  ;
;
для частки:  .
.
Гранична помилка вибірки при типовому відборі завжди менша помилки при власне-випадковому відборі, тому що групова дисперсія менше загальної дисперсії.
5.При серійному (гніздовому) відборі кожна з відібраних серій розглядається як одиниця сукупності.
Мірою коливаннь є міжсерійна вибіркова дисперсія ( ), тобто середній квадрат відхилень серійних вибіркових середніх від загальної вибіркової середньої:
), тобто середній квадрат відхилень серійних вибіркових середніх від загальної вибіркової середньої:
 ,
,
де  – середня по кожній серії;
– середня по кожній серії;
 – загальна вибіркова середня;
– загальна вибіркова середня;
 – число відібраних серій.
– число відібраних серій.
Гранична помилка середньої при серійному повторному відборі:  ;
;
помилка частки:  .
.
6.При серійному безповторном у відборі:
для середньої:  ;
;
для частки:  ,
,
де  – міжсерійна дисперсія;
– міжсерійна дисперсія;
 – число відібраних серій (у вибірковій сукупності);
– число відібраних серій (у вибірковій сукупності);
 – число серій у генеральній сукупності.
– число серій у генеральній сукупності.