МЕТОД НАЛОЖЕНИЯ (СУПЕРПОЗИЦИИ)

Этот метод основан на принципе наложения, который утверждает: ток в любой ветви линейной электрической цепи, содержащей несколь­ко источников ЭДС, равен алгебраической сумме токов в этой ветви при действии каждого источника в отдельности. При этом остальные источ­ники заменяются резисторами, имеющими сопротивления, равные внут­ренним сопротивлениям замененных источников ЭДС.

Справедливость этого принципа следует непосредственно выражения:

Действительно, если в этом выражении положить все ЭДС, кро­ме Е₁, равным нулю, то получим частичный ток I^/к в К-й ветви, вызванный действием только ЭДС. E₁

Если считать Е2 ≠ 0, а осталь­ные ЭДС равны нулю, то получим частичный ток I^//_К, вызванный действием только ЭДС Е₂ и т. д.

Алгебраическая сумма всех частич­ных токов даст действительный ток, протекающий в к-й ветви.

Принцип наложения применим и к напряжениям, так как они линейно связаны с токами. К расчету же мощности этот принцип применять нельзя, так как мощность является не линейной, а квад­ратичной формой тока или напряжения: если по участку цепи с сопротивлением R протекает ток I = I₁ + I₂, то мощность равна:

Р = RI² = R (I₁ + I₂)²

а не RI₁² + RI₂², как формально следовало бы из принципа наложе­ния.

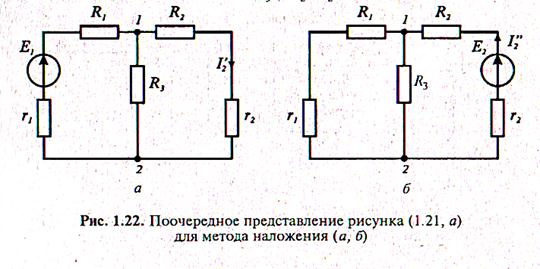Вывод: метод наложения позволяет найти токи в ветвях без составления и решения системы уравнений, а непосредственно по закону Ома. При этом вначале находят частичные токи от действия каждого ис­точника ЭДС в отдельности, принимая остальные ЭДС равными нулю и оставляя в схеме только их внутренние сопротивления, а затем — действительные токи как алгебраические суммы частичных токов.