МЕТОД КОНТУРНЫХ ТОКОВ

N - 1.

Недостающее уравнение можно получить на основании второго закона Кирхгофа. Для контура abcf при обходе по часовой стрелке:

Если направление обхода контура совпадает с направлением ЭДС и токов, то эти ЭДС и соответствующие падания напряжений берутся со знаком «плюс».

При составлении уравнений по второму закону Кирхгофа контуры нужно выбирать так, чтобы каждый из них отличался хотя бы одной ветвью.

Вывод: метод уравнений Кирхгофа сводится к со­ставление системы уравнений в соответствии с первым и вторым законами Кирхгофа и решение этой системы относительно неизве­стных токов.

Если электрическая цепь содержит «В» ветвей, то в об­щем случае необходимо определить «В» токов, т. е. токи в каждой из ветвей. Следовательно общее число уравнений по первому и второ­му законам Кирхгофа должно быть равно «В».

При числе узлов «У» - число независимых уравнений по первому закону Кирхгофа будет «У – 1», следовательно, остальные «П» уравнений должны быть составлены по второму закону Кирхгофа:

П = В - (У - 1).

Общее число уравнений, составленных по первому и второму законам Кирхгофа, равно числу ветвей, т. е. числу неизвестных то­ков; это позволяет найти токи во всех ветвях электрической цепи.

Если сложная цепь содер­жит довольно много узлов и контуров, то ее расчет с помощью первого и второго законов Кирхгофа будет связан с решением большого числа уравнений. Вводя понятие о контурных токах, можно свести уравнения, составленные по законам Кирхгофа, к системе урав­нений, составленных только для независимых конту­ров.

Под контурными токами понимают условные токи, замыкающиеся в соответствующих контурах.

Контурный ток обозначается буквой I с римским индексом, отвечающим номеру независимого контура. Контурный ток равен току в ветви, по которой он протекает индивидуально.

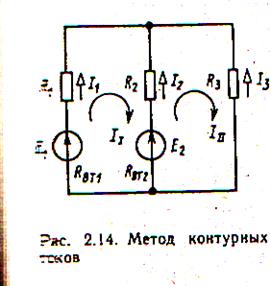
Рассмотрим схему цепи, представленную на рис. 2.14.

Эта схема имеет два независимых контура I и II, в каждом из которых проходят токи I₁ и I₁₁. На­правления этих токов выбирается произвольными, на­пример по часовой стрелке. Из рассмотрения схемы (рис. 2.14) видно, что реальные токи во внешних вет­вях равны контурным: I₁ = I₁ I₃ = I₁₁

Ток во внутрен­ней ветви равен разности контурных токов: I₂ = I₁ - I₁₁

Для определения контурных токов составим два уравнения:

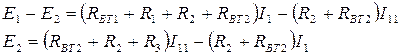
Собственным сопротивлением контура называется сумма всех сопротивлений в каждом независимом контуре.

Собственное сопротивление обозначается буквой R с двойным индексом соответственно номеру того контура, к которому относится.

Взаимным сопротивлением контуров называется сопротивление, входящее одновременно в каждый из двух смежных контуров.

Взаимное сопротивление обозначается буквой R с двумя индексами соответственно номерам смежных контуров.

Контурной ЭДС называется алгебраическая сумма всех ЭДС в каждом независимом контуре.

Вывод: метод контурных токов сводится к составлению и решению системы уравнений, получаемых только по второму закону Кирхгофа применительно к понятиям контурных токов, сопротивлений и ЭДС.

МЕТОД УЗЛОВОГО НАПРЯЖЕНИЯ.

 

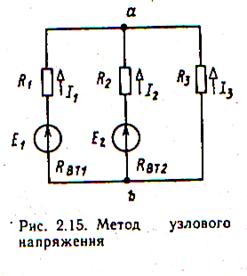
Часто в сложной цепи имеется всего два узла, как, например, в схеме рис. 2.14. В этом случае расчет цепи значительно упрощается, так как достаточно определить так называемое узловое напряжение U_аб.(рис.2.15) После этого токи в ветвях находятся следующим образом:

 

Все токи в ветвях направляются к узлу, потенциал которого условно принимается за нуль. Узловое напряжение:

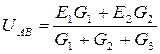
где G – проводимость соответствующих ветвей.

Если ЭДС источника направлена к узлу, то произведение ЕG берется со знаком «минус». Токи в ветвях определяются так:

 

Вывод: метод узлового напряжения сводится к составлению системы уравнений, составленных только по первому закону Кирхгофа; из этих уравнений определяются напряжения в узлах схемы электрической цепи относительно некоторого базисного узла, потенциал которого изначально принимается равным нулю, а токи в ветвях, соединяющих узлы, находят по закону Ома.