Решение задачи 1
Исходные данные
Задание 1
1. Построить линейное уравнение парной регрессии;
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации;
3. Оценить статистическую зависимость параметров регрессии и корреляции (с помощью F-критерия Фишера и Т-статистики Стьюдента).
Задание 2
1. Построить уравнение парной регрессии в виде нелинейной функции: степенной у = ахb, экспоненты у = аеbх, показательной у = abx, любой на выбор;
2. Для оценки параметров модель линеаризируется путем логарифмирования или потенцирования;
3. Определяется коэффициент эластичности и индекс корреляции;
4. Значимость определяется по критерию Фишера.
Исходные данные для решения задач приведены в таблице 1.
Таблица 1 - Исходные данные
| N | X | Y |
Решение задачи 1
Определим линейное уравнение парной регрессии.
Для этого составим и решим следующую систему уравнений:
;
.
;
.
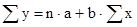Решая данную систему уравнений получаем:
а=81,232;
b=0,76.
Итого получаем: 
Рассчитаем линейные коэффициенты парной корреляции и среднюю ошибку аппроксимации
Расчет будем вести табличным способом, и представим в таблице 2.
Таблица 2 - Расчет линейных коэффициентов парной корреляции и средняя ошибка аппроксимации
| N | X | Y | X∙Y | X2 | Y2 |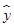 
| Y-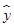
| 
| 
|
| 98,71 | 11,29 | 127,42 | 10,26 | ||||||
| 115,43 | 9,57 | 91,55 | 7,65 | ||||||
| 107,07 | 3,93 | 15,43 | 3,54 | ||||||
| 119,99 | 1,01 | 1,02 | 0,83 | ||||||
| 102,51 | 6,49 | 42,09 | 5,95 | ||||||
| 128,35 | -1,35 | 1,83 | 1,06 | ||||||
| 135,19 | 7,81 | 60,96 | 5,46 | ||||||
| 129,11 | -8,11 | 65,80 | 6,70 | ||||||
| 134,43 | 19,57 | 382,91 | 12,71 | ||||||
| 115,43 | -7,43 | 55,23 | 6,88 | ||||||
| 119,99 | 16,01 | 256,26 | 11,77 | ||||||
| 101,75 | 7,25 | 52,53 | 6,65 | ||||||
| 128,35 | -3,35 | 11,24 | 2,68 | ||||||
| 124,55 | -14,55 | 211,76 | 13,23 | ||||||
| 129,11 | -9,11 | 83,03 | 7,59 | ||||||
| 133,67 | 0,33 | 0,11 | 0,24 | ||||||
| 137,47 | -6,47 | 41,89 | 4,94 | ||||||
| 107,83 | -2,83 | 8,02 | 2,70 | ||||||
| 97,19 | -23,19 | 537,87 | 31,34 | ||||||
| 126,83 | -6,83 | 46,68 | 5,69 | ||||||
| ∑ | 2093,62 | 147,90 | |||||||
| Ср. | 50,55 | 119,65 | 6263,5 | 2838,45 | 14584,35 | 119,65 | 104,68 | 7,39 |
На рисунке 1 представим поле корреляции.
Рисунок 1 - Поле корреляции
Оценим статистическую зависимость параметров регрессии и корреляции (с помощью F-критерия Фишера и Т-статистики Стьюдента).
Определение коэффициента корреляции
Для определения коэффициента корреляции, определим дисперсию:
;
.
Определим коэффициент корреляции:
.
Данный коэффициент корреляции характеризует высокую тесноту связи
Определим коэффициент детерминации:
Это значит, что 61% вариации "у" объясняется вариацией фактор "х".
Определение статистической значимости уравнения регрессии с помощью F-критерия Фишера
Определим F- критерий Фишера:
.
Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы 1 и (20-2)=18 составляет Fтаб = 4,45.
Имеем F> Fтаб, следовательно уравнение регрессии признается статистическим значимым.
Оценка статистической значимости параметров регрессии с помощью t-статистики Стьюдента
Табличное значение t-критерия для числа степеней свободы df=n-2=20-2=18 и уровня значимости α=0,05 составит tтабл=1,743.
Определим стандартные ошибки:
;
;
.
Тогда
;
;
.
Фактические значения t-статистики превосходят табличное значение:
, поэтому параметры а, b, и rxy не случайно отличаются от нуля, а статистически значимы.
Рассчитаем доверительные интервалы для параметров регрессии а и b. Для этого определим предельную ошибку для каждого показателя:
;
.
Получаем доверительные интервалы:
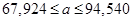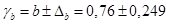и 
;
и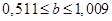 
.
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью р=1-α=1-0,05=0,95 параметры а и b, находятся в указанных границах, не принимают нулевых значений, т.е. являются статистически значимыми и существенно отличны от нуля.