Доверительные интервалы

 

Доверительная вероятность γ - вероятность того, что доверительный интервал накроет действительное значение параметра, оцениваемого по выборочным данным.

В математических рассуждениях в рассматриваемой методической разработке, т.е. для стандартного нормального распределения, в формулах для границ доверительного интервала используют множитель:

U( 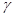) = Ф^-1( ).

Если 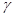= 0,95, то

Ф^-1( ) = Ф^-1(0,975) = 1,96 = U( ),

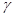Если γ = 0,99, то

Ф^-1( ) = Ф^-1(0,995) = 2,58 = U( ).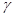

См. таблицы функции, обратной к функции стандартного нормального распределения.

 

При n → ∞ имеем асимптотическое сближение распределения x*(t) с нормальным распределением, а потому ширина асимптотического доверительного интервала равна:

2 U( ) .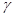

Если выбрано 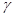= 0,95, то это значит, что в 95% случаев условное математическое ожидание точечного прогноза x*(t), т.е. значение x(t), будет находиться внутри доверительного интервала и только в 5% случаев – вне его. При γ = 0,95 имеем U(γ) =1,96.

Если мы хотим, чтобы в 99 случаях из 100 условное математическое ожидание попадало в рассматриваемый интервал со случайными границами, необходимо этот интервал расширить (при γ = 0,99 имеем U(γ) = 2,58). Но при этом уменьшается точность прогнозирования.

Поясним на примере. Пусть задача - прогнозирование погоды в Москве через год. Рассмотрим прогноз – температура будет от (-50⁰С) до (+70⁰С). Увеличили ширину доверительного интервала до 140⁰С, и можно утверждать, что этот прогноз сбудется с вероятностью γ = 1, т.е. надежность этого прогноза 100%. Но точность этого прогноза невелика.

Если уменьшим γ , то доверительный интервал можно сузить, при этом точность прогноза увеличится. Например, значению γ = 0,9 соответствует U(γ) = 1,64.

На основе опыта конкретных научных и прикладных работ принято в социально-экономических исследованиях использовать γ =0,95 и U(γ) = 1,96.

 

Рассмотрим наиболее распространенные ошибки при расчетах интервального прогноза.

1. При расчете доверительного интервала берут вместо коэффициента U(γ) величину γ и не умножают на σ^* - оценку среднего квадратичного отклонения погрешности измерения. Напомним, что необходимо использовать выражение:

δ = U( ) .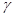

Т.е. вместо произведения U(γ)σ^* ошибочно берут просто доверительную вероятность γ .

2. Проверкой правильности вычислений можно считать равенство значений знаменателя в формуле, задающей оценку а^* , т.е.

и знаменателя под корнем при расчете доверительных интервалов - тоже:

Отметим, что

= -

Доказательство. Справедливо тождество

= .

Поскольку

,

о

,

что и следовало доказать.