Теорема об изменении кинетической энергии системы.

Рис.50

Рис.49

При повороте на конечный угол работа будет равна

,

а в случае постоянного момента

.

Рисунок 27

Если на тело действует пара сил, лежащая в плоскости, перпендикулярной к оси Оz, то Мz будет, очевидно, означать момент этой пары.

Укажем еще, как в данном случае определяется мощность

.

Следовательно, при действии сил на вращающееся тело мощность равна произведению вращающего момента на угловую скорость тела. При той же самой мощ­ности вращающий момент будет тем больше, чем меньше угловая скорость.

3) Работа сил трения, действующих на катя­щееся тело. На колесо ра­диуса R (рис.50), катящееся по некоторой плоскости (поверх­ности) без скольжения, действует сила трения F , препятствующая скольжению точки касания В вдоль плоскости. Элементарная работа этой силы . Но точка В в данном случае является мгновенным центром скоростей и . Так как , то и для каждого элементарного перемещения .

 

Следовательно, при качении без скольжения, работа силы тре­ния, препятствующей скольжению, на любом перемещении тела равна нулю. По той же причине в этом случае равна нулю и работа нормальной реакции N, если считать тела недеформируемыми и силу N приложенной в точке В (как на рис.50,а).

Сопротивление качению, возникающее вследствие деформации поверх­ностей (pис.50,б), создает пару (), момент которой , где k- коэффициент трения качения. Тогда учитывая, что при качении угол поворота колеса , получим:

,

где - элементарное перемещение центра С колеса.

Если N= const, то полная работа сил сопротивления качению будет равна

Так как величина мала, то при наличии других сопротивлений сопротивлением качению можно в первом приближении пренебрегать.

 

Если рассмотреть какую-нибудь точку системы с мас­сой , имеющую скорость , то для этой точки будет

,

где и - элементарные работы действующих на точку внеш­них и внутренних сил. Составляя такие уравнения для каждой из точек системы и складывая их почленно, получим

,

или

. (2)

Равенство выражает теорему об изменении кине­тической энергии системы в дифференциальной форме.

Если полученное выражение отнести к элементарному промежутку времени, в течение которого произошло рассматриваемое перемещение, можно получить вторую формулировку для дифференциальной формы теоремы: производная по времени от кинетической энергии механической системы равна сумме мощностей всех внешних () и внутренних () сил, т.е.

.

Дифференциальными формами теоремы об изменении кинетической энергии можно воспользоваться для составления дифференциальных уравнений движения, но это делается достаточно редко, потому что есть более удобные приемы.

Проинтегрировав обе части равенства (2) в пределах, соответствующих перемещению системы из некоторого начального положения, где кинетическая энергия равна , в положение, где значение кинетической энергии становится равным , будемиметь

.

Полученное уравнение выражает теорему об изменении кинетической энергии в конечном виде: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом пере­мещении всех приложенных к системе внешних и внутренних сил.

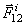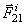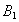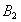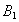В отличие от предыдущих теорем, внутренние силы в уравнениях не исключаются. В самом деле, если и - силы взаимодействия между точками и системы (см. рис.51), то . Но при этом точка , может перемещаться по направ­лению к 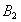, а точка 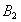- по направлению к 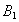. Работа каждой из сил бу­дет тогда положительной и сумма работ нулем не будет. Примером мо­жет служить явление отката. Внутренние силы (силы давления), действующие и на снаряд и на откатывающиеся части, совершают здесь положительную работу. Сумма этих работ, не равная нулю, и изменяет кинетическую энергию системы от вели­чины в начале выстрела до величины конце.

Другой пример: две точки, соединенные пружиной. При изменении расстояния между точками упругие силы, приложенные к точкам, будут совершать работу. Но если система состоит из абсолютно твердых тел и связи между ними неизменяемые, не упругие, идеальные, то работа внутренних сил будет равна нулю и их можно не учитывать и вообще не показывать на расчетной схеме.

Рассмотрим два важных частных случая.

1) Неизменяемая система. Неизменяемой будем называть систему, в которой расстояния между точками приложения внутрен­них сил при движении системы не изменяются. В частности, такой системой является абсолютно твердое тело или нерастяжимая нить.