Некоторые случаи вычисления работы.

Рис.48

Рис.47

Рис.46

 

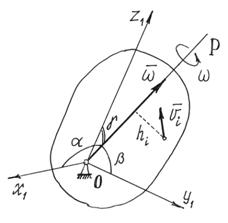
При вращении тела вокруг неподвижной точки кинетическая энергия определяется как (рис.47)

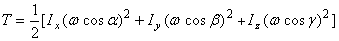
или, окончательно,

,

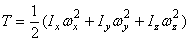где I_x, I_y, I_z – моменты инерции тела относительно главных осей инерции x₁, y₁, z₁ в неподвижной точке О ; 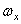, 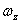_, – проекции вектора мгновенной угловой скорости на эти оси.

 

3. Плоскопараллельное движение. При этом движе­нии скорости всех точек тела в каждый момент времени распреде­лены так, как если бы тело вращалось вокруг оси, перпендикулярной к плоскости движения и проходящей через мгновенный центр ско­ростей Р (рис.46). Следовательно

,

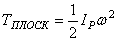где 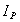- момент инерции тела относительно названной выше оси, w- угловая скорость тела. Величина 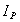в формуле будет перемен­ной, так как положение центра Р при движе­нии тела все время меняется. Введем вместо 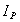постоянный момент инерции 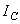, относительно оси, проходящей через центр масс С тела. По теореме Гюйгенса 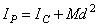, где d=PC. Подставим это выражение для 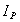. Учитывая, что точка Р - мгновенный центр скоростей, и, следовательно, 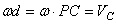, где 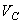- скорость центра масс С, окончательно найдем:

.

Следовательно, при плоскопараллельном движении кинетиче­ская энергия тела равна энергии поступательного движения со скоростью центра масс, сло­женной скинетической энергией вращательного движения вокруг центра масс.

4) Для самого общего случая движения материальной системы кинетическую энергию помогает вычислить теорема Кенига.

Рассмотрим движение материальной системы как сумму двух движений (рис.48). Переносного – поступательного движения вместе с центром масс С и относительного – движения относительно поступательно движущихся вместе с центром масс осей x₁, y₁, z_1. Тогда скорость точек 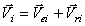. Но переносное движение – поступательное. Поэтому переносные скорости всех точек равны, равны 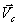. Значит, и кинетическая энергия будет

 

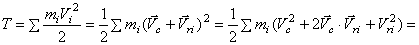
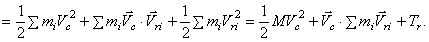
По определению центра масс его радиус-вектор в подвижной системе 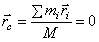(центр масс находится в начале координат), значит, и . Производная по времени от этой суммы также равна нулю:

.

Поэтому, окончательно, кинетическая энергия системы

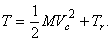(1)

Кинетическая энергия материальной системы равна сумме кинетической энергии при поступательном движении вместе с центром масс и кинетической энергии ее при движении относительно координатных осей, поступательно движущихся вместе с центром масс.

В общем случае движения тела, которое можно рассматривать как сумму двух движений (переносного – поступательного вместе с центром масс С и относительного – вращения вокруг точки С), по теореме Кенига (1) получим

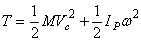или ,

где I_x, I_y, I_z – главные центральные оси инерции тела.

 

1) Работа сил тяжести, действующих на систему. Работа силы тяжести, действующей на частицу весом 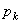, будет равна 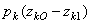, где и 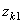- координаты, определяющие начальное и конечное положение частицы. Тогда сумма работ всех сил тяжести, действующих на систему, будет равна

,

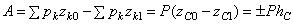где Р - вес системы, - вертикальное перемещение центра тяжести (или центра масс). Следовательно, работа сил тяжести, действую­щих на систему, вычисляется как работа их равнодействую­щей Р на перемещении центра тяжести (или центра масс) системы.

2) Работа сил, приложенных к вращающемуся телу. Элементарная работа приложенной к телу силы F (рис.49) будет равна

,

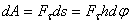так как 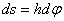, где 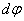- угол поворота тела.

Но, как легко видеть, . Будем называть величину вращающим моментом. Тогда получим: .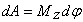

Следовательно, в рассматриваемом случае элементарная работа равна произведению вращающего момента на элементарный угол поворота. Формула справедлива и при действии нескольких сил, если считать 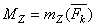.