Дифференциальные уравнения движения точки
Рис. 3
Рис.2
Рассмотрим «динамическое равновесие» точки. Его так называют потому, что на самом деле точка не находится в равновесии, она движется с ускорением.
На точку действуют силы: вес 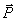 и натяжение нити
и натяжение нити  , реакция нити. Приложим к точке ее силу инерции
, реакция нити. Приложим к точке ее силу инерции 
 , направленную в сторону противоположную ускорению точки и автомобиля, и составим уравнение равновесия:
, направленную в сторону противоположную ускорению точки и автомобиля, и составим уравнение равновесия:

Рис. 13.1.
Из второго уравнения следует 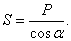
Из первого  и
и 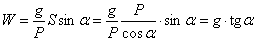 .
.
Пример 2.Лифт весом Р (рис.3) начинает подниматься с ускорением  . Определить натяжение троса.
. Определить натяжение троса.

Рассматривая лифт как свободный, заменяем действие связи (троса) реакцией Т и, составляя уравнение 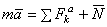 в проекции на вертикаль, получаем:
в проекции на вертикаль, получаем:
 .
.
Отсюда находим:  .
.
Если лифт начнёт опускаться с таким же ускорением, то натяжение троса будет равно:
 .
.
С помощью дифференциальных уравнений движения решается вторая задача динамики. Правила составления таких уравнений зависят от того, каким способом хотим определить движение точки.
1) Определение движения точки координатным способом.
Рассмотрим свободную материальную точку, движущуюся под действием сил  ,
, ,..,
,..,  . Проведем неподвижные координатные оси Oxyz (рис.4). Проектируя обе части равенства
. Проведем неподвижные координатные оси Oxyz (рис.4). Проектируя обе части равенства  на эти оси и учитывая,что
на эти оси и учитывая,что  и т.д., получим дифференциальные уравнения криволинейного движения точки в проекциях на оси прямоугольной декартовой системы координат:
и т.д., получим дифференциальные уравнения криволинейного движения точки в проекциях на оси прямоугольной декартовой системы координат:
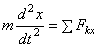 ,
,  ,
, 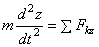 .
.
