Вынужденные колебания системы.
Рис.84
Рис.83
Следует заметить, что колебательный процесс не будет периодическим. Но, так как система проходит через положение равновесия через равное время, все-таки вводят понятие периода 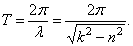
Если сравнить этот период колебаний с периодом колебаний системы без сопротивления (3), увидим, что сопротивление увеличивает период колебаний и уменьшает их частоту.
Интересна закономерность изменения амплитуды. Найдем отношение соседних амплитуд (через полпериода 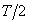 ):
):
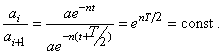
То есть амплитуды уменьшаются по закону геометрической прогрессии, знаменателем которой является величина  .
.
Натуральный логарифм ее, равный 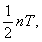 называется логарифмическим декрементом колебаний.
называется логарифмическим декрементом колебаний.
Конечно, через период амплитуда уменьшится в 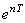 раз, а через m периодов – в
раз, а через m периодов – в 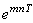 раз.
раз.
б) Случай большого сопротивления (n>k).
Корни характеристического уравнения получатся вещественными: 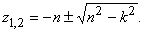 В этом случае, как известно из курса математики, решение дифференциального уравнения (10):
В этом случае, как известно из курса математики, решение дифференциального уравнения (10):
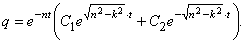 (13)
(13)
Решение явно неколебательное, непериодическое.
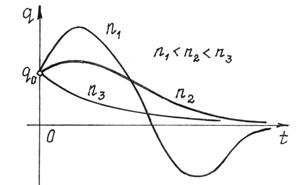
Графики таких движений показаны на рис.84. Вид движения зависит от начальных условий и величины коэффициента сопротивления n.
в) Случай равного сопротивления (n = k).
Корни характеристического уравнения получаются равными: 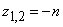 . Поэтому решение дифференциального уравнения
. Поэтому решение дифференциального уравнения
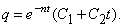 (14)
(14)
Движение и в этом случае не будет колебательным.
Если сила, которая вывела систему из положения равновесия, продолжает действовать, то такое колебание не будет свободным, будет вынужденным. И эта сила называется возмущающей силой.
Рассмотрим колебательное движение под действием обобщенной возмущающей силы, изменяющейся по гармоническому закону 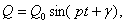 где
где 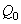 - максимальная величина возмущающей силы; р – частота изменения силы;
- максимальная величина возмущающей силы; р – частота изменения силы;  – начальная фаза изменения силы.
– начальная фаза изменения силы.
Дифференциальное уравнение вынужденных колебаний получится таким
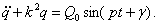 (15)
(15)
Решение этого линейного неоднородного дифференциального уравнения состоит из общего решения соответствующего однородного уравнения и частного решения. Общее решение уже было получено в (7) или (8). Частное решение ищем в виде 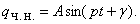
Подставив его в дифференциальное уравнение (15), получим
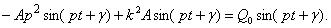 Отсюда
Отсюда
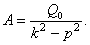 (16)
(16)
Значит полное решение уравнения (15)
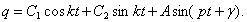 (17)
(17)
Так как общее и частное решения совершаются с разными частотами, то вынужденные колебания не будут гармоническими. Но, как нам уже известно, общее решение определяет свободные колебания, которые с течением времени довольно быстро затухают. Поэтому интерес представляют только установившиеся колебания:
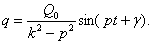 (18)
(18)
Отсюда следует, что установившиеся вынужденные колебания будут гармоническими с частотой р, равной частоте возмущающей силы и, что они не зависят от начальных условий.
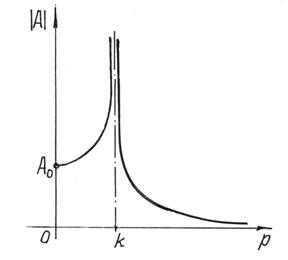
И, самое интересное, – амплитуда колебаний А зависит от частоты р возмущающей силы. График этой зависимости дан на рис.85.