Расчет средних значений и дисперсии одномерного признака

Предварительный анализ данных одномерных признаков

Прежде всего, по данным одномерного признака, рассчитываются две статистические характеристики: среднее значение и дисперсия.

Среднее значение является оценкой математического ожидания случайной величины. Запишем формулу расчета среднего значения признака в принятых обозначениях. Форму для расчета среднего первого признака таблицы данных будет иметь вид:

(3.1)

Оценка дисперсии признака первого признака производится по формуле:

(3.2)

В пакете EXCEL расчет среднего значения производится с помощью функции СРЗНАЧ. При вызове функции указывается диапазон ячеек таблицы данных, для которого необходимо рассчитать среднее значение. В нашем случае один из столбцов таблицы данных (рис. 3.1).

В пакете EXCEL расчет оценки дисперсии признака производится с помощью функции ДИСП. При вызове функции указывается диапазон ячеек таблицы данных, для которого необходимо рассчитать оценка. В нашем случае один из столбцов таблицы данных (рис. 3.2). В EXCEL есть еще одна функция расчета дисперсии. Это функция ДИСПР. Отличие этой функции заключается в том, что в формуле 3.2 деление производится не на величину n-1 , а на величину n.

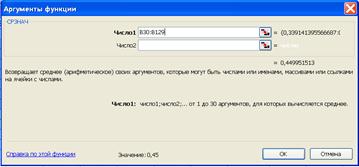
Рис. 3.1. Диалоговое окно функции СРЗНАЧ

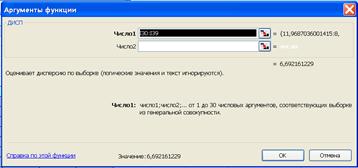
Рис. 3.2. Диалоговое окно функции ДИСП

На ряду с дисперсией для характеристики случайных признаков используется такая характеристика как среднеквадратичное отклонение. Среднеквадратичное отклонение связано с дисперсией соотношением:

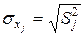(3.3)

Для вычисления квадратного корня в EXCEL математическая функция КОРЕНЬ.