Основные понятия об эконометрических моделях и корреляционном анализе.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
Таразский государственный университет им. М.Х. Дулати
УТВЕРЖДАЮ
Заведующий кафедрой
___________________________________
___________________________________
_________________ ________________________
/подпись/ /Ф.И.О./
«_____»_______________200__г.
Методическое указание
Для выполнения __________________________________________
/наименование работы/
________________________________________________________________________________
/наименование дисциплины/
для студентов специальности_______________________________________________________
/шифр и наименование специальности/
_______________________________________________________
Тараз 20___
Методические указания для выполнения _______________________________________
/практических, лабораторных работ, РГЗ, ДЗ, КП/КР/
по дисциплине ___________________________________________________________________
/наименование дисциплины/
________________________________________________________________________________
для студентов специальности_______________________________________________________
________________________________________________________________________________
_________________________________________ разработаны в соответствии с типовой учебной программой дисциплины.
Методические указания разработаны: ____________________________________________
/Ф.И.О., должность, уч. ст., уч. зв./
________________________________________________________________________________
________________________________________________________________________________
Методические указания обсуждены на заседании кафедры
________________________________________________________________________________
/наименование кафедры/
Протокол №______ от «_____» __________________20___г.
Лабораторная работа №1
Основные понятия об эконометрических моделях и корреляционном анализе.
Эконометрические модели являются составляющими более широкого класса ЭММ. Данная модель выступает в качестве средств анализа и прогнозирования конкретных экономических процессов, как на макро, так и на микро уровнях на основе реальной статистики.
Эконометрическая модель, учитывая корреляционные связи, позволяет путем подбора аналитической зависимости построить модель на базисном периоде и при достаточной адекватности модели использовать ее для краткосрочного прогноза.
При синтезе эконометрических моделей при имеющихся факторных признаках xi и результативных параметрах yi необходимо определить a0, a1, a2, a3, …,an.
yi = f(xi) + ei, где
f(xi) – величина детерминированная; ei, yi – величины случайные.
Эконометрическая модель опирается на понятие корреляционных связей и так называемое уравнение регрессии.
Корреляционная связь – когда при одном и том же значении факторного признака х встречаются разные значения у. Корреляционные связи описываются так называемыми уравнениями регрессии.
Уравнение регрессии – уравнение прямой (как и любой кривой), описывающее корреляционную связь, а сама прямая (кривая) называется линией регрессии.
Корреляционные связи оцениваются по среднему значению всей совокупности результативного признака, такт как для одного и того же значения факторного признака возможны различные значения результативного признака.
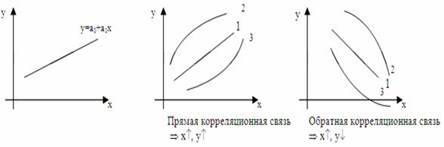
Корреляционные связи (уравнения регрессии), а также эконометрические модели, построенные на базе уравнения регрессии, могут описываться:
1)уравнением прямой: yi = a0 + a1x
2)уравнением 2-го порядка: yi = a0 + a1x + a2x2
3)уравнением показательной функции: yi = a0a1x
4)уравнением степенной функции: yi = a0xa1
5)уравнением гиперболы: yi = a0 + a11/x
При построении эконометрических моделей нам известны фактические значения х и у, а нам необходимо определить параметры a0 , a1, a2 для соответствующей модели. Данные параметры определяются по методу наименьших квадратов.
Лабораторная работа №2
Метод наименьших квадратов (МНК).
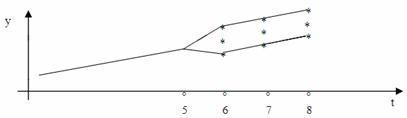
Суть данного метода заключается в том, что квадрат суммы разностей между фактическим значением результативного признака и его теоретическим значением сводится к минимуму.
F = (уфакт – утеор )2 min
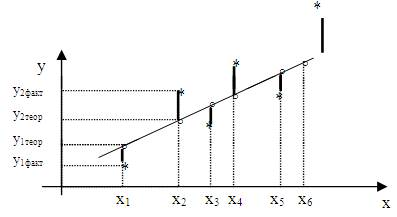
* - уфакт (эмпирическое)
Чтобы найти параметры a0 , a1, a2 , необходимо в формулу (1) подставить утеор, то есть ту аналитическую зависимость, которой будем сглаживать (аппроксимировать) статистический материал. Как известно из математики для нахождения минимума функции нужно взять частные производные по анализируемым параметрам, то есть ... и приравнять данное выражение к нулю. Получим систему нормальных уравнений, из которых найдем заданные коэффициенты.
F = (уфакт – a0 – a1xфакт)2 min
Урасч = a0 + a1xфакт
(*)
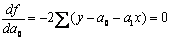преобразовав уравнение (*), получим систему нормальных уравнений:
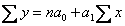
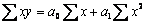
решением системы (**) будут:
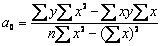
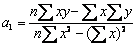
Рассчитав коэффициенты a0 , a1, можно синтезировать модель:
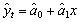(оценки коэффициентов a0 , a1)
Аналогичным образом используя МНК, можно получить коэффициенты для остальных функций, используемых при аппроксимации.
Если в качестве факторного признака х используется время t, то такой ряд называется динамическим (временным) рядом. При применении специального подхода при обозначении факторного признака t, когда сумма времени t будет равна 0, выражения для коэффициентов a0 , a1 , a2 – будут проще.
ti, t = 0
| -2 | -1 |
При таком подходе формулы коэффициентов a0 , a1 значительно упрощаются:
, 
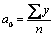(для линейной функции)
Аналогично определяем коэффициенты для других функций:
yt =a0 +a1t +a2t2 (парабола)
алуым керек
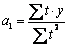
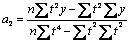
y =a0 a1t (показательная функция)
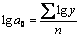
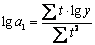
Для того, чтобы убедится, что полученные коэффициенты являются типичными, используют метод оценки с помощью распределения Стьюдента (критерий Стьюдента). Находят:
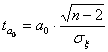
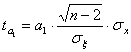
s - среднее квадратичное отклонение;
2 – дисперсия
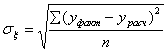- остаточная дисперсия
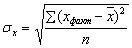
Отделив ta0, ta1 и сравнив с tтабличное, можно сделать вывод, что если ta0 tтабличное и
ta1 tтабличное (ta0 tтабличное ta1), то параметры а0 и а1 – стандартно типичны (обладают оценкой несмещенной, эффективной).
Получив синтезированные модели по функциям 1-5 срвнивают остаточную диперсию и по минимальности остаточной диперсии выбирают функцию для аппроксимации (сглаживания).
Для оценки прогноза используют обычно не дискретные (точечные) значения результативного признака, а рассчитанный интервал.
Упрогнозное = Утеор t*
- коэффициент доверия, обычно выбирается 0,05 и вероятность Р=0,95.
t - находится по таблице Стьюдента (t = 4,3).
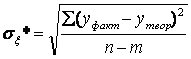
sx* - скорректированное среднее квадратичное отклонение с учетом степеней свободы n - m, где
m - число параметров нашей синтезируемой модели;
n - объем выборки.
Для y =a0 +a1x, m = 2
Лабораторная работа №3