Внутренняя энергия
Легко видеть, что запись (2.3) противоречит закону сохранения энергии. В самом деле, если, например, ударять по тяжёлому неподвижному телу и/или нагревать его, то оно останется неподвижным, т.е. ни кинетическая, ни потенциальная энергии тела не изменятся, в то время как работа и/или теплота не равны нулю. Это говорит о том, что любая термодинамическая система, кроме механических видов энергии, должна обладать ещё одним видом энергии, её назвали внутренней энергией U, таким образом, что закон сохранения энергии принимает вид:
 (2.4)
(2.4)
По современным представлениям внутренняя энергия тела складывается из всех видов энергий всех частиц, составляющих систему.
Таким образом, если система как целое остаётся неподвижной при воздействии на неё окружающей среды, то изменяется её внутренняя энергия. Обычно I начало термодинамики записывают для неподвижных систем и формулируют следующим образом: теплота, подведённая к системе, затрачивается на изменение её внутренней энергии и на совершение ею работы. Если система переходит из начального состояния (1) в конечное состояние (2), то I начало записывается в виде:
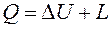 . (2.5)
. (2.5)
Если начальное и конечное состояния дифференциально близки, то I начало записывается в дифференциальной форме:
 , (2.6)
, (2.6)
где  есть малые величины теплоты и работы в процессе, а
есть малые величины теплоты и работы в процессе, а  - малое изменение внутренней энергии. I начало термодинамики требует, чтобы внутренняя энергия U системы была однозначной функцией состояния, а её дифференциал полным. В самом деле, если бы
- малое изменение внутренней энергии. I начало термодинамики требует, чтобы внутренняя энергия U системы была однозначной функцией состояния, а её дифференциал полным. В самом деле, если бы  не был полным дифференциалом, т.е. если бы внутренняя энергия U не была однозначной функцией состояния, то при совершении кругового процесса (цикла) появлялся бы излишек (положительный или отрицательный) внутренней энергии, что приводило бы к возможности построения вечного двигателя I рода.
не был полным дифференциалом, т.е. если бы внутренняя энергия U не была однозначной функцией состояния, то при совершении кругового процесса (цикла) появлялся бы излишек (положительный или отрицательный) внутренней энергии, что приводило бы к возможности построения вечного двигателя I рода.
I начало может быть записано для удельных величин:
 . (2.7)
. (2.7)
В случае простых систем, для которых  , имеем:
, имеем:
 (2.8)
(2.8)
Если в качестве независимых параметров системы выбрать температуру T и удельный объём v, то полный дифференциал внутренней энергии будет записываться в виде:
 . (2.9)
. (2.9)
2.3. Энтальпия. Полезная внешняя работа
Запишем I начало термодинамики для неподвижной простой системы:

и применим к этому выражению преобразование Лежандра:
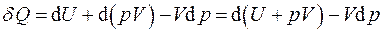 .
.
Здесь под знаком полного дифференциала появляется новая функция состояния:

 , (2.10)
, (2.10)
называемая энтальпией. Таким образом, первое начало термодинамики может быть записано в двух эквивалентных формах:
 (2.11)
(2.11)
Физический смысл энтальпии может быть выяснен из смысла произведения  . Рассмотрим следующий пример. Пусть в вертикально расположенном цилиндре под поршнем находится газ (рис.2.1). На поршень давит груз весом G = Mгрg. Если груз вместе с поршнем неподвижны, значит, на поршень снизу действует давление со стороны газа, равное
. Рассмотрим следующий пример. Пусть в вертикально расположенном цилиндре под поршнем находится газ (рис.2.1). На поршень давит груз весом G = Mгрg. Если груз вместе с поршнем неподвижны, значит, на поршень снизу действует давление со стороны газа, равное  , где f - площадь поршня. Это выражение может быть записано в виде
, где f - площадь поршня. Это выражение может быть записано в виде  . Умножив левую и правую части этого равенства на высоту h положения поршня от дна цилиндра, получим
. Умножив левую и правую части этого равенства на высоту h положения поршня от дна цилиндра, получим  . Произведение же
. Произведение же  есть потенциальная энергия груза в поле тяжести Земли.
есть потенциальная энергия груза в поле тяжести Земли.

Таким образом, произведение pV представляет собой в рассмотренном случае потенциальную энергию поршня вместе с грузом, удерживающего газ в заданном объёме V. В общем случае, если система удерживается в объёме V, потенциальная энергия оболочки, удерживающей систему, равняется произведению pV.
Следовательно, энтальпиюнужно понимать как энергию расширенной термодинамической системы, включающей в себя саму систему и оболочку, удерживающую систему в заданном объёме.
В результате преобразования Лежандра, кроме энтальпии появилось ещё одно слагаемое - (-Vdp), имеющее смысл дифференциально малого количества некоторой работы  , т.е.:
, т.е.:
 . (2.12)
. (2.12)
Интеграл:
 (2.13)
(2.13)
носит название полезной внешней работы.
Графически полезная внешняя работа L', определяемая интегралом (2.14), изображается площадью слева от кривой зависимости p(V) в координатах p - V ( рис.2.2).
Запишем также полный дифференциал удельной энтальпии, выбрав в качестве независимых переменных T и p системы:
 . (2.14)
. (2.14)
 |
2.4. Теплоёмкость простой термодинамической системы
Запишем математическое выражение I начала термодинамики для простой системы в двух формах (2.11) (с использованием внутренней энергии и энтальпии) в развёрнутом виде с учётом полных дифференциалов для внутренней энергии (2.9) и энтальпии (2.14) и определения количества теплоты (1.4):
 (2.15)
(2.15)
Будем поддерживать постоянным объём системы, т.е. положим  Такой процесс называется изохорным. Тогда, т.к. теплоёмкость системы зависит от процесса, следует положить
Такой процесс называется изохорным. Тогда, т.к. теплоёмкость системы зависит от процесса, следует положить  . Из первого уравнения (2.15) получаем
. Из первого уравнения (2.15) получаем
 , (2.16)
, (2.16)
т.е. теплоёмкость при постоянном объёме есть изменение внутренней энергии системы при изменении температуры на единицу при поддержании постоянным её объёма.
Аналогичным образом, рассмотрев изобарный процесс, т.е. процесс при постоянном давлении  получим определение теплоёмкости при постоянном давлении:
получим определение теплоёмкости при постоянном давлении:
 , (2.17)
, (2.17)
т.е. теплоёмкость при постоянном давлении есть изменение энтальпии тела при изменении температуры на единицу при поддержании постоянным давления.
На основании (2.15) теплоёмкость произвольного термодинамического процесса может быть записана в двух эквивалентных формах (делим обе части уравнения на dT):
 (2.18)
(2.18)
Далее мы увидим, что теплоемкость зависит от того, какой термодинамический процесс происходит.