Поиск оптимальных смешанных стратегий
Пусть дана платежная матрица A[mxn] = aij[mxn], у которой не существует цена игры, т.е. α≠β, α<β. Величина α – та величина, которая не может быть больше гарантированного среднего выигрыша игрока А, если он при повторении игры все время будет выбирать стратегию максимина.
Ставится вопрос: можно ли найти величину V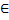 (α,β), чтобы изменяя выбор своей стратегии игрок А гарантировал себе средний выигрыш не меньше чем V.
(α,β), чтобы изменяя выбор своей стратегии игрок А гарантировал себе средний выигрыш не меньше чем V.
Теорема (Основная теорема теории игр с нулевой суммой): Любая игра [mxn] с нулевой суммой имеет пару оптимальных смешанных стратегий (S*A,S*B), обладающих свойством устойчивости: Если игрок будет придерживаться своей оптимальной стратегии, то другому игроку невыгодно отступать от своей оптимальной стратегии при многократном повторении игры.
Смешанной стратегией игрока А называется вектор SA=(p1,p2,…pm), где pi – вероятность случайного выбора стратегии Ai. SB=(q1,q2,…qn) – смешанная стратегия игрока В, qi – вероятность случайного выбора стратегии Bj игроком B.
Условия:  (1);
(1); 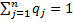 (2)
(2)
Предполагая, что существует некоторая величина V ниже которой не может быть средний выигрыш игрока А, независимо от выбора игроком В своей стратегии получим, что для вектора SA должны выполняться неравенства: 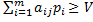 (3)
(3)
Обозначим pi/V := xi, i=1,..m (4). Тогда (3) запишется в виде: 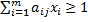 (5). Введем функцию
(5). Введем функцию  (6). z=1/V – величина, обратная среднему выигрышу игрока А, при условии, что он будет придерживаться стратегии SA.
(6). z=1/V – величина, обратная среднему выигрышу игрока А, при условии, что он будет придерживаться стратегии SA.
Т.к. игрок А заинтересован в том, чтобы получить максимально возможный средний выигрыш V, то учитывая выражение (6) игрок А должен решать задачу  (7) при условии, что
(7) при условии, что 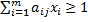 (8),
(8),  (9), i=1,..m. Задача (7),(8),(9) является задачей линейного программирования.
(9), i=1,..m. Задача (7),(8),(9) является задачей линейного программирования.
Если рассмотреть задачу со стороны игрока В и обозначить yj=qj/V, j=1,..n (10), то получим задачу 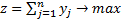 (11), при условиях
(11), при условиях 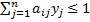 (12), i=1,..m,
(12), i=1,..m,  (13), j=1,..n.
(13), j=1,..n. 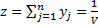 (14), а игрок В стремится минимизировать величину V, т.к. V – средний выигрыш игрока А. Неравенство (12) получаются из условий
(14), а игрок В стремится минимизировать величину V, т.к. V – средний выигрыш игрока А. Неравенство (12) получаются из условий 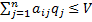 (15), означающих, что средний проигрыш игрока В при любом выборе стратегии игрока А будет не больше величины V.
(15), означающих, что средний проигрыш игрока В при любом выборе стратегии игрока А будет не больше величины V.
Таким образом, получены две задачи - (7),(8),(9) и (11),(12),(13), образующие пару двойственных задач линейного программирования.
Пример (Решение игры в три пальца)
Не существует чистой стратегии ни для какого из игроков. Будем искать оптимальные смешанные стратегии. К элементам платежной матрицы добавим число M=5 так, чтобы все элементы этой матрицы были неотрицательны. Доказано, что при этом смешанные стратегии SA,SB не изменятся, а цена игры увеличится на М. V’=V+M
| B1 | B2 | B3 | |
| A1 | |||
| A2 | |||
| A3 |
Запишем задачу (7),(8),(9) для этой матрицы: 
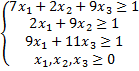
Эта задача решается симплекс-методом. В результате будет найдено оптимальное решение: x1*=1/20, x2*=1/10, x3*=1/20. z*=1/20+1/10+1/20=1/5. Следовательно, 1/V'=z*=1/5, V'=5, V*=5-5=0
Т.е. оптимальный средний выигрыш игрока равен 0, если игрок B будет придерживаться оптимальной стратегии. p1*=x1*·V’=5/20=1/4, p2*=5/10=1/2, p3*=5/20=1/4. Следовательно, оптимальная смешанная стратегия для игрока А задается S*A=(1/4, ½ , ½).
Для игрока B аналогично записывается задача (11),(12),(13) и ее решение будет: S*B=(1/4, ½ , 1/4).
Понятие о двойственных задачах линейного программирования
Пусть дана задача линейного программирования в стандартной форме: 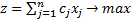 (1).
(1).
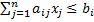 , i=1,..m (2)
, i=1,..m (2) 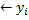
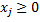 , j=1,..n (3)
, j=1,..n (3)
Для перехода к двойственной задаче вводятся новые переменные yi, i=1,..m. При этом любая переменная yi соответствует одному из неравенств (2). После этого записывается двойственная задача в следующем виде: