Простая линейная регрессия

Пусть X и Y одномерные величины; обозначим их х и .у, а функция f(x,Q) имеет вид f(x,Q) = a+bx, где Q = (a, b). Относительно имеющихся наблюдений (x_i, y_i), i = 1,..., n, полагаем, что

y_i = a + bx_i + e_i (2)

где e₁,…e_n- независимые одинаково распределенные случайные величины, определяющие действие различных неучтенных факторов на изменение результирующего показателя Y.

Уравнение (2) определяет простую (парную) линейную регрессию. Можно различными методами подбирать "лучшую" прямую линию, изменяя параметры a и b. На практике широко используется метод наименьших квадратов (МНК), суть которого заключается в следующем.

Построим оценку параметра Q = (a, b) так, чтобы величины

e_i = y_i – f(x_i, Q) = y_i – a - bx_i

называемые остатками, были как можно меньше, а именно, чтобы сумма их квадратов была минимальной:

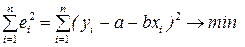(3)

Сумму минимимизируем по (а,b),приравнивая нулю производные по аи b.В результате получим систему уравнений линейных относительно aи b. Ее решение легко находится:

(4) и (5)

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции r_yx. Для линейной регрессии (-1≤r_yx≤1)

r_yx = bσ_x/σ_y

σ_x₌ , σ_y₌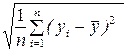

и индекс корреляции ρ_yx – для нелинейной регрессии (0≤ρ_yx≤1)

ρ_yx = , ,

где - дисперсия результирующего показателя y; - дисперсия отклонений наблюдаемых значений результирующего показателя y_i от рассчитанных по уравнению регрессии .

Качество построенной модели можно оценить с помощью коэффициента (индекса) детерминации:

R² = = = ρ²_yx,

здесь - дисперсия, объясняемая регрессией. Чем больше значение этого показателя ( а оно изменяется от 0 до 1), тем лучше уравнение регрессии объясняет рассеяние наблюдаемых значений результирующего показателя y относительно средней величины, тем меньшее влияние на это рассеяние оказывают случайные факторы. Это видно из соотношения:

Задача дисперсионного анализа состоит в анализе дисперсии результирующего показателя.

Для получения несмещенной оценки дисперсии случайной величины сумму квадратов отклонений от среднего значения делят не на число наблюдений – n, а на число степеней свободы – df.

Число степеней свободы равно разности между числом неизвестных наблюдений случайной величины и числом связей, ограничивающих свободу их изменений, т. е. числом уравнений, связывающих эти наблюдений.