Линейный регрессионный анализ

 

В линейный регрессионный анализ входит широкий круг задач, свя­занных с построением (восстановлением) зависимостей между группами чи­словых переменных

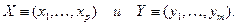
Предполагается, что X - независимые переменные (факторы, объяс­няющие переменные) влияют на значения Y - зависимых переменных (результирующих, объясняемых переменных). По имеющимся эмпирическим данным (x_i, y_i), i = 1,...,n (n – число наблюдений) требуется построить функцию f(X), которая приближенно описывала бы изменение Y при изменении X:

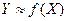
Предполагается, что множество допустимых функций, из которого подбирается f(X), является параметрическим:

f(X) =f(X,Q ),

где Q - неизвестный параметр (вообще говоря, многомерный). При построении f(X) будем считать, что

Y = f(X,Q )+e, (1)

 

где первое слагаемое - закономерное изменение Y от X, а второе - e - случай­ная составляющая с нулевым средним. f(X,Q ) является условным математическим ожиданием Y при условии известного X и называется рег­рессией Y no X.