Решение задачи линейного программирования геометрическим методом
Задача использования сырья
Для производства двух видов изделий 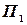 и
и  используются три вида сырья:
используются три вида сырья:  Запасы сырья ограничены. Предприятие обеспечены сырьем первого вида в количестве
Запасы сырья ограничены. Предприятие обеспечены сырьем первого вида в количестве  кг., сырьем второго вида в количестве
кг., сырьем второго вида в количестве 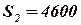 кг., сырьем третьего вида в количестве
кг., сырьем третьего вида в количестве  кг.
кг.
На производство одного изделия 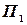 необходимо затратить сырья первого вида -
необходимо затратить сырья первого вида -  кг., сырья второго вида -
кг., сырья второго вида - 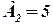 кг., сырья третьего вида -
кг., сырья третьего вида -  кг. На производство одного изделия
кг. На производство одного изделия  необходимо затратить сырья первого вида -
необходимо затратить сырья первого вида -  кг., сырья второго вида -
кг., сырья второго вида -  кг., сырья третьего вида -
кг., сырья третьего вида -  кг.
кг.
Прибыль от реализации одного изделия 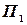 составляет
составляет  тыс. руб., а изделия
тыс. руб., а изделия  -
-  тыс. руб.
тыс. руб.
Составить план производства изделий 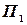 и
и  так, чтобы предприятие получило наибольшую прибыль от реализации.
так, чтобы предприятие получило наибольшую прибыль от реализации.
Решение:
Обозначим через  количество изделий
количество изделий  , через
, через  - количество изделий
- количество изделий  . Тогда на все изделия
. Тогда на все изделия  понадобиться
понадобиться  кг. сырья первого вида. Всего
кг. сырья первого вида. Всего  кг. По условию сырья первого вида 3000 кг. Значит, мы получаем первое неравенство
кг. По условию сырья первого вида 3000 кг. Значит, мы получаем первое неравенство
 .
.
Знак неравенства поставлен ввиду того, что сырье может использоваться не полностью.
Аналогично, по сырью второго вида получаем неравенство  ,
,
а по сырью третьего вида
 .
.
Прибыль от реализации  изделий
изделий  и
и  изделий
изделий  равна
равна
 .
.
Мы получаем математическую модель задачи:
Найти: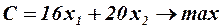
При условиях: 
Алгоритм;
1. Строим прямые, которые получаются в результате замены в ограничениях знаков неравенств на знаки равенств.
2. Находим полуплоскости, определяемые каждым из ограничений задачи.
3. Находят многоугольник решений 9это множество точек пересечения полуплоскостей полученных в пункте 2).
4. Строят вектор  .
.
5. Строим прямую 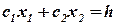 , проходящую через многоугольник решений.
, проходящую через многоугольник решений.
6. Передвигаем прямую 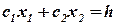 в направлении вектора
в направлении вектора  , в результате чего находят точку (точки), в которых целевая функция принимает максимальное значение (это последняя точка общая с многоугольником решений).
, в результате чего находят точку (точки), в которых целевая функция принимает максимальное значение (это последняя точка общая с многоугольником решений).
Если прямую передвигаем в направлении противоположном  , то находим точку (точки) в которых целевая функция принимает минимальное значение (это последняя точка общая с многоугольником решений).
, то находим точку (точки) в которых целевая функция принимает минимальное значение (это последняя точка общая с многоугольником решений).
Либо устанавливаем неограниченность функции.
7. Определяем координаты точки максимума (минимума) функции и вычисляем значение целевой функции в этой точке.