Формулировка принципа максимума.

Вводится функция

, (3.2)

где - правые части уравнений движения (1.1), 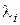- множители Лагранжа, удовлетворяющие уравнениям

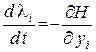(3.3)

с граничными условиями

(3.4)

Исходная система (1.1), (1.2) может быть представлена в виде

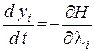, (3.5)

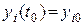, (3.6)

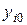- заданные величины.

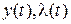В соответствие с (3.1) – (3.5) функция при фиксированных является функцией управления и ее можно исследовать на минимум или максимум.

Будем говорить, что удовлетворяет условию максимума функции H если при фиксированных для любого времени t выполняется условие

(3.7)

Тогда справедливо следующее утверждение.

Если управление доставляет минимум функционалу (3.1), то оно удовлетворяет условию максимума (3.7), где 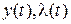определяются из системы уравнений (3.3), (3.4), (3.5), (3.6) при управлении , найденном из условия максимума (3.7).

Из формулировки принципа максимума следует, что он является необходимым условием абсолютного минимума. Принцип максимума, сформулированный академиком Понтрягиным Л.С. , позволяет получить замкнутую систему уравнений (3.2) – (3.7) для определения оптимального управления и соответствующего ему решения.

Следует отметить, что в соответствие с принципом максимума задача минимизации функционала сводится к задаче минимизации функции и решению краевой задачи.

Замечание 1. В том случае, когда время 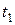не фиксировано, полученная система соотношений принципа максимума должна быть дополнена условием трансверсальности, которое имеет вид

которое используется для определения оптимального времени процесса .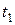

Замечание 2. В общем случае принцип максимума дает необходимые условия абсолютного минимума . Можно доказать, что в случае линейных систем с линейным или квадратичным функционалом принцип максимума дает и достаточные условия оптимальности.

Замечание 3. В том случае, когда конечные значения заданы (правый конец несвободен) допустимыми являются не все возможные функции 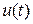, а только те из них, которые приводят траекторию в заданное состояние. Поэтому из доказательства принципа максимума со свободным правым концом не следует его справедливость для систем с фиксированными концами. Тем не менее оказывается, что условия принципа максимума выполняются и в этом случае, за исключением граничных условий для множителей Лагранжа.

Пример 1. Пусть уравнение движения имеет вид

(3.8)

и минимизируется

, где 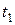- некоторое заданное время. В данном случае

(3.9)

Из условия стационарности

следует

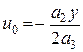. (3.10)

Таким образом, решение сводится к краевой задаче (3.8), (3.9), (3.10) для определения , и соответствующих 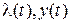. Окончательное суждение об оптимальности найденного управления можно сделать по знаку второй производной . В нашем случае

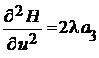Если 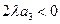, то найденное управление доставляет минимум .

Пример 2. Пусть уравнение движения имеет вид

- задано

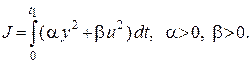
Вводя новую переменную у₂

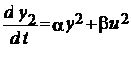
перейдем от задачи Лагранжа к задаче Майера

В этом случае

( переменную y рассматриваем как у₁)

Тогда и удовлетворяют системе управлений с граничными условиями

;

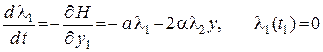Оптимальное управление находится из условия максимума функции H по u. Из условия

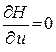находим

Так как , то , а - находится из краевой задачи.

При этом

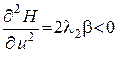, значит найденное управление доставляет максимум функции H и дает решение поставленной задачи.

Пример 3. Пусть уравнение движения имеет вид

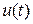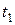- задано требуется найти управление , минимизирующее при условии, что - задано, а управление ограничено .

В этом случае 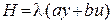. Тогда из условия максимума функции H по u следует, что

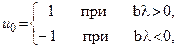
т.е. .

Для определения l имеем уравнение

Пусть a –постоянна положительная величина.

Тогда 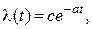из условия следует . Тогда .

Так как отрицательна,

т.е. не влияет на величину оптимального управления, а влияет только на знак его.

3.3. Задача на максимальное быстродействие.

В системе

(3.11)

требуется найти управление, переводящее систему из одного (заданного) состояния в другое (конечное) состояние за минимальное время , т.е. в данном случае

Рассмотрим решение этой задачи на основе принципа максимума. Для определенности положим .

В соответствии с принципом максимума функционал качества необходимо представить в форме Майера: .

Для этого введем переменную с помощью уравнения

Тогда .

Введем функцию , где множители Лагранжа удовлетворяют уравнению с неизвестными начальными и конечными значениями.

Из структуры H видно, что

Тогда дальнейшее исследование функции H сводится к исследованию .

Дальнейшее решение проведем для системы, описывающейся уравнением

. (3.12)

Перепишем уравнение (3.12) в форме системы дифференциальных уравнений

(3.13)

Требуется перевести систему (3.13) из состояния

в начало координат ( y₁₁=y₂₁=0) за минимальное время.

В данном случае

где

Решая систему уравнений, найдем

Будем считать, что.

Из условия максимума функции H следует, что

Учитывая, что - линейная функция меняющее знак не более одного раза, оптимальное управление может быть: или с одним переключением.

Предположим, что , тогда

- константы интегрирования.

На фазовой плоскости получим уравнение . Различным значениям будут соответствовать различные фазовые траектории (параболы).

И только при фазовая траектория проходит через начало координат. Поэтому с уравнением можно попасть в начало координат только, стартуя с фазовой траектории 0А.

Пусть теперь .

В этом случае

и .

Видно, что с управлением можно попасть в начало координат только стартуя с точек фазовой траектории B0.

Таким образом, фазовая плоскость делится линией A0B на 2 части (области D и C).

Есть старт с точек области D, то сначала , затем .

Если же – c точек области C, то

Линия A0B – линия переключения.

Так реализуется оптимальное управление в задаче быстродействия.