Вводные замечания.

Принцип максимума Понтрягина.

Рассмотрим исходную постановку задачи оптимального управления, заключающуюся в поиске такой управляющей функции 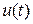и соответствующей траектории , удовлетворяющей системе (1.1), (1.2), на которых некоторый функционал достигает минимального значения.

Функции 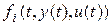предполагаются непрерывными по и дважды непрерывно дифференцируемыми по остальным аргументам. Оптимальное управление отыскивается в классе кусочно-непрерывных функций с конечным числом точек разрыва, со значением из некоторой замкнутой или открытой выпуклой области U r – мерного пространства. При этом фазовые координаты в точках разрыва управления остаются непрерывными. В качестве критерия оптимальности рассматривается функционал Майера

, (3.1)

где t₁ – заданное конечное время управления. В рассматриваемом случае начальное состояние считается заданным, а - свободным, т.е. рассматривается задача со свободным правым концом.

Если в вариационном исчислении минимум отыскивается среди близких кривых сравнения (- малые по мере 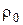или ), то в принципе максимума вариации управления могут быть конечными, но из заданной области.

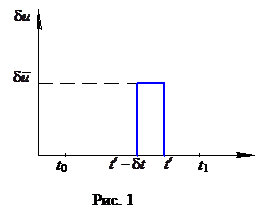Вводится понятие игольчатой вариации

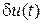здесь не малые, но влияние 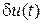на управляемое движение малое, т.е. 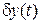, обусловленное воздействием 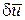мало в силу малости времени его воздействия . Малым будет и приращение функционала. Использование игольчатых вариаций позволяет получить более сильные условия - необходимые условия абсолютного минимума (максимума).