Задачі регресійного аналізу

Регресійний аналіз

Основна особливість регресійного аналізу: при його допомозі можна отримати конкретні відомості про те, яку форму і характер має залежність між досліджуваними змінними.

Послідовність етапів регресійного аналізу

Розглянемо коротко етапи регресійного аналізу.

Формулювання задачі. На цьому етапі формуються попередні гіпотези про залежність досліджуваних явищ.
Визначення залежних і незалежних (що пояснюють) змінних.
Збір статистичних даних. Дані повинні бути зібрані для кожної із змінних, включених в регресійну модель.
Формулювання гіпотези про форму зв'язку (проста або множинна, лінійна або нелінійна).
Визначення функції регресії (полягає в розрахунку чисельних значень параметрів рівняння регресії)
Оцінка точності регресійного аналізу.
Інтерпретація отриманих результатів. Отримані результати регресійного аналізу порівнюються з попередніми гіпотезами. Оцінюється коректність і правдоподібність отриманих результатів.
Передбачення невідомих значень залежної змінної.

За допомогою регресійного аналізу можливе вирішення задачі прогнозування і класифікації. Прогнозні значення обчислюються шляхом підстановки в рівняння регресії параметрів значень пояснюючих змінних. Вирішення задачі класифікації здійснюється таким чином: лінія регресії ділить всю множину об'єктів на два класи, і та частина множини, де значення функції більше нуля, належить до одного класу, а та, де вона менше нуля, – до іншого класу.

Розглянемо основні задачі регресійного аналізу: встановлення форми залежності, визначення функції регресії, оцінка невідомих значень залежної змінної.

Встановлення форми залежності.

Характер і форма залежності між змінними можуть утворювати наступні різновиди регресії:

Ø позитивна лінійна регресія (виражається в рівномірному зростанні функції);

Ø позитивна рівноприскорена зростаюча регресія;

Ø позитивна рівносповільнена зростаюча регресія;

Ø негативна лінійна регресія (виражається в рівномірному падінні функції);

Ø негативна рівноприскорена спадаюча регресія;

Ø негативна рівносповільнена спадаюча регресія.

Проте описані різновиди зазвичай зустрічаються не в чистому вигляді, а в поєднанні один з одним. В такому разі говорять про комбіновані форми регресії.

Визначення функції регресії.

Друга задача зводиться до з'ясування дії на залежну змінну головних чинників або причин, за незмінних інших рівних умов, і за умови виключення дії на залежну змінну випадкових елементів. Функція регресії визначається у вигляді математичного рівняння того або іншого типу.

Оцінка невідомих значень залежної змінної.

Вирішення цієї задачі зводиться до вирішення задачі одного з типів:

Ø Оцінка значень залежної змінної усередині даного інтервалу вихідних даних, тобто пропущених значень; при цьому вирішується задача інтерполяції.

Ø Оцінка майбутніх значень залежної змінної, тобто знаходження значень поза заданим інтервалом вихідних даних; при цьому вирішується задача екстраполяції.

Обидві задачі вирішуються шляхом підстановки в рівняння регресії знайдених оцінок параметрів значень незалежних змінних. Результат вирішення рівняння є оцінкою значення цільової (залежною) змінної.

Розглянемо деякі припущення, на які спирається регресійний аналіз.

Припущення лінійності, тобто передбачається, що зв'язок між даними змінними є лінійним. Так, в даному прикладі ми побудували діаграму розсіювання і змогли побачити явний лінійний зв'язок. Якщо ж на діаграмі розсіювання змінних ми бачимо явну відсутність лінійного зв'язку, тобто присутній нелінійний зв'язок, слід використовувати нелінійні методи аналізу.

Припущення про нормальність залишків. Воно допускає, що розподіл різниці передбачених і спостережуваних значень є нормальним. Для візуального визначення характеру розподілу можна скористатися гістограмами залишків.

При використанні регресійного аналізу слід враховувати його основне обмеження. Воно полягає в тому, що регресійний аналіз дозволяє виявити лише залежності, а не зв'язки, що лежать в основі цих залежностей.

Регресійний аналіз дає можливість оцінити міру зв'язку між змінними шляхом обчислення передбачуваного значення змінної на підставі декількох відомих значень.

Рівняння регресії.

Рівняння регресії виглядає таким чином: Y = a + b·x

За допомогою цього рівняння змінна Y виражається через константу а і кут нахилу прямої (або кутовий коефіцієнт) b, помножений на значення змінної X. Константу а також називають вільним членом, а кутовий коефіцієнт – коефіцієнтом регресії або B- коефіцієнтом.

У більшості випадків (якщо не завжди) спостерігається певний розкид спостережень відносно регресійної прямої.

Залишок – це відхилення окремої крапки (спостереження) від лінії регресії (передбаченого значення).

Для вирішення задачі регресійного аналізу в MS Excel вибираємо в меню Сервис "Пакет анализа" і інструмент аналізу "Регрессия". Задаємо вхідні інтервали X і Y. Вхідний інтервал Y – це діапазон залежних аналізованих даних, він повинен включати один стовпець. Вхідний інтервал X – це діапазон незалежних даних, які необхідно проаналізувати. Число вхідних діапазонів должно бути не більше 16.

На виході процедури у вихідному діапазоні отримуємо звіт, наведений в таблиці 8.3а, – 8.3в.

ПІДВЕДЕННЯ ПІДСУМКІВ

Таблиця 8.3а. Регресійна статистика

Регресійна статистика
Множественный R	0,998364
R-квадрат	0,99673
Нормированный R-квадрат	0,996321
Стандартная ошибка	0,42405
Наблюдения

Спочатку розглянемо верхню частину розрахунків, представлену в таблиці 8.3а, – регресійну статистику.

Величина R-квадрат, називається також мірою визначеності, характеризує якість отриманої регресійної прямої. Ця якість виражається мірою відповідності між вихідними даними і регресійною моделлю (розрахунковими даними). Міра визначеності завжди знаходиться в межах інтервалу [0;1].

В більшості випадків значення R-квадрат знаходиться між цими значеннями, називаються екстремальними, тобто між нулем і одиницею.

Якщо значення R-квадрата близьке до одиниці, це означає, що побудована модель пояснює майже всю мінливість відповідних змінних. І навпаки, значення R-квадрата, близьке до нуля, означає погану якість побудованої моделі.

У нашому прикладі міра визначеності дорівнює 0,99673, що говорить про дуже хорошу підгонку регресійної прямої до вихідних даних.

Множественный R – коефіцієнт множинної кореляції R – виражає міру залежності незалежних змінних (X) і залежної змінної (Y).

Множественный R дорівнює квадратному кореню з коефіцієнта детермінації, ця величина набуває значень в інтервалі від нуля до одиниці.

У простому лінійному регресійному аналізі множественный R дорівнює коефіцієнту кореляції Пірсона. Дійсно, множественный R в нашому випадку дорівнює коефіцієнту кореляції Пірсона з попереднього прикладу (0,998364).

Таблиця 8.3б. Коефіцієнти регресії

	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	2,694545455	0,33176878	8,121757129
Переменная X 1	2,305454545	0,04668634	49,38177965
* Приведений усічений варіант розрахунків

Тепер розглянемо середню частину розрахунків, представлену в таблиці 8.3б. Тут надано коефіцієнт регресії b (2,305454545) і зсув по осі ординат, тобто константа а (2,694545455).

Виходячи з розрахунків, можемо записати рівняння регресії таким чином:

Y = x·2,305454545 + 2,694545455

Напрям зв'язку між змінними визначається на підставі знаків (негативний або позитивний) коефіцієнтів регресії (коефіцієнта b).

Якщо знак при коефіцієнті регресії – позитивний, зв'язок залежної змінної з незалежною буде позитивним. У нашому випадку знак коефіцієнта регресії позитивний, отже, зв'язок також є позитивним.

Якщо знак при коефіцієнті регресії – негативний, зв'язок залежної змінної з незалежною є негативним (зворотною).

У таблиці 8.3в. представлені результати виведення залишків. Для того, щоб ці результати з'явилися в звіті, необхідно при запуску інструменту "Регрессия" активувати чекбокс "Остатки".

ВИВЕДЕННЯ ЗАЛИШКУ

Таблиця 8.3в. Залишки

Наблюдение	Предсказанное Y	Остатки	Стандартные остатки
	9,610909091	– 0,610909091	– 1,528044662
	7,305454545	– 0,305454545	– 0,764022331
	11,91636364	0,083636364	0,209196591
	14,22181818	0,778181818	1,946437843
	16,52727273	0,472727273	1,182415512
	18,83272727	0,167272727	0,418393181
	21,13818182	– 0,138181818	– 0,34562915
	23,44363636	– 0,043636364	– 0,109146047
	25,74909091	– 0,149090909	– 0,372915662
	28,05454545	– 0,254545455	– 0,636685276

За допомогою цієї частини звіту ми можемо бачити відхилення кожної крапки від побудованої лінії регресії. Найбільше абсолютне значення залишку в нашому випадку – 0,778, найменше – 0,043. Для кращої інтерпретації цих даних скористаємося графіком вихідних даних і побудованою лінією регресії, представленими на рис. 8.3. Як бачимо, лінія регресії досить точно "підігнана" під значення вихідних даних.

Слід враховувати, що даний приклад є досить простим і далеко не завжди можлива якісна побудова регресійної прямої лінійного вигляду.

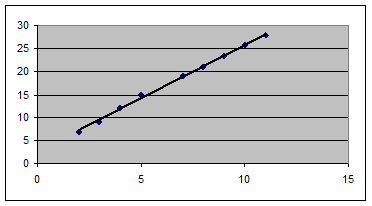
Рис. 8.3. Вихідні дані і лінія регресії

Залишилося нерозглянутим задача оцінки невідомих майбутніх значень залежної змінної на підставі відомих значень незалежної змінної, тобто задача прогнозування.

Маючи рівняння регресії, задача прогнозування зводиться до вирішення рівняння Y = x·2,305454545 + 2,694545455 з відомими значеннями x. Результати прогнозування залежної змінної Y на шість кроків вперед представлені в таблиці 8.4.

Таблиця 8.4. Результати прогнозування змінної Y

х	Y(прогнозоване)
	28,05455
	30,36
	32,66545
	34,97091
	37,27636
	39,58182

Таким чином, в результаті використання регресійного аналізу в пакеті Microsoft Excel ми:

Ø побудували рівняння регресії;

Ø встановили форму залежності і напрям зв'язку між змінними – позитивна лінійна регресія, яка виражається в рівномірному зростанні функції;

Ø встановили напрям зв'язку між змінними;

Ø оцінили якість отриманої регресійної прямої;

Ø змогли побачити відхилення розрахункових даних від даних вихідного набору;

Ø передбачили майбутні значення залежної змінної.

Якщо функція регресії визначена, інтерпретована і обґрунтована, і оцінка точності регресійного аналізу відповідає вимогам, можна вважати, що побудована модель і прогнозні значення володіють достатньою надійністю.

Прогнозні значення, отримані в такий спосіб, є середніми значеннями, які можна чекати.