Волновое уравнение

 

Колебательные процессы всегда описываются решениями дифференциальных уравнений второго порядка. Найдем дифференциальное уравнение, решения которого описывают распространение синусоидальной волны, задаваемой формулой (4.57). Найдем вторые производные S по t и x.

;

.

Отсюда следует равенство

, (4.60)

которое является искомым одномерным волновым уравнением. Для случая распространения волны в трехмерном пространстве можем обобщить уравнение (4.60)

. (4.61)

Это уравнение можно записать с использованием оператора Лапласа:

. (4.62)

Для записи решения уравнения (4.61), соответствующего плоской волне с произвольным направлением распространения, введем волновой вектор, по модулю равный волновому числу k и направленный вдоль луча в рассматриваемой точке М среды. Волновой вектор плоской синусоидальной волны не зависит от выбора точки М, и уравнение такой волны можно записать в форме

, (4.63)

где 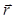— радиус-вектор точки М, а α - начальная фаза колебаний в начале координат, т. е. в точке 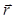=0. Отметим, что скалярное произведение

,

где r_k – проекция радиус-вектора на направление волнового вектора. Очевидно, что проекции всех радиус-векторов, задающих точки плоскости, перпендикулярной волновому вектору, равны между собой и фаза колебаний во всех точках плоскости одинакова. Плоскости, перпендикулярные вектору , являются волновыми поверхностями и формула (4.63) действительно описывает плоскую волну, направление распространения которой задает вектор .

Проверим, действительно ли уравнение (4.63) есть решение уравнения (4.61). Для этого, используя свойства скалярного произведения векторов и 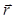, запишем выражение (4.63) в виде

, (4.63)

где k_x, k_y, k_z – декартовские составляющие вектора . Вторые производные S по координатам имеют вид

;

;

.

Подстановка этих выражений в выражение (4.61) превращает уравнение в тождество

.

Остается отметить, что решением уравнения (4.61) должна являться любая функция вида

. (4.63)

В этом можно легко убедиться подстановкой функции в уравнение. Таким образом, решения уравнения (4.61) соответствуют распространению не только синусоидальных волн, но и модулированных волн, переносящих информацию.