Радиус-вектор. Перемещение. Траектория. Пройденный путь
Основные понятия механики
ЛЕКЦИЯ 1. КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ
МЕХАНИКА
Предметом изучения механики является механическое движение, которое заключается в изменении с течением времени взаимного расположения тел или их частей в пространстве. Всякое движение происходит относительно какого-либо тела, которое называется телом отсчёта. С телом отсчёта связывают систему координат, с помощью которой задается положение движущегося тела. Совокупность тела отсчёта, связанной с ним системы координат и часов, отсчитывающих время, называется системой отсчёта. Относительно разных систем отсчета движение одного и того же тела выглядит по-разному. В этом заключается относительность движения. При решении практических задач систему отсчета необходимо выбирать так, чтобы движение рассматриваемого тела было наиболее простым, т.е. описывалось наименьшим числом уравнений.
Для математического описания движения различных тел используют математические модели. Мы будем пользоваться моделями материальной точки и абсолютно твёрдого тела. Материальной точкой называется тело, размерами которого в условиях данной задачи можно пренебречь. Положение материальной точки в общем случае задается тремя декартовыми координатами – x, y и z. Абсолютно твёрдым называется тело, деформациями которого можно пренебречь при рассмотрении его движения. Для задания положения абсолютно твердого тела в пространстве достаточно знать координаты двух точек этого тела.
Как уже говорилось выше, положение материальной точки можно задать с помощью трех декартовых координат или с помощью радиус-вектора  , который проводится из начала координат в ту точку пространства, в которой находится материальная точка (рис. 1.1), причём
, который проводится из начала координат в ту точку пространства, в которой находится материальная точка (рис. 1.1), причём
 , (1.1)
, (1.1)
где  – единичные векторы в направлении соответствующих осей x, y, z.
– единичные векторы в направлении соответствующих осей x, y, z.

Рисунок 1.1 – Положение материальной точки в пространстве
При движении точки М изменяются с течением времени как её координаты, так и радиус-вектор. Потому для задания закона движения точки необходимо указать либо зависимость изменения координат со временем
x = x(t), y = y(t), z = z(t),(1.2)
либо зависимость
 . (1.3)
. (1.3)
Уравнения (1.2) и (1.3) называются кинематическими уравнениями движения материальной точки.
Введём некоторые определения. Траекторией называют воображаемую линию, которую описывает в пространстве материальная точка при её движении. Расстояние между точками 1 и 2 (рис. 1.2), отсчитанное вдоль траектории, называется пройденным путём.
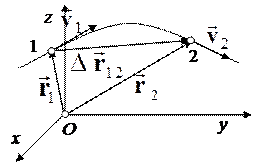
Рисунок 1.2 – Перемещение
Пройденный путь – величина скалярная. Вектор, проведенный из начальной точки траектории в конечную, называется перемещением:
 .
.
Из определения вектора перемещения имеем, что
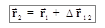 ,
,
т.е. положение материальной точки в данной системе отсчета определено, если известно ее начальное положение – вектор  и перемещение
и перемещение  .
.