Постановка ЗЛП, различные формы записи. Примеры экономических задач.

Линейное программирование – раздел математического программирования, рассматривающий задачи оптимизации линейных функций многих переменных при линейных ограничениях на область изменения переменных.

Особенностью ЗЛП является то, что линейная целевая функция не имеет экстремума и достигает наибольшего или наименьшего значения на границе допустимой области.

Рассмотрим постановку ЗЛП на примере задачи и наилучшем использовании ресурсов. Имеется m видов ресурсов в ограниченном количестве b = (b₁, b₂, … , b_m). Ресурсы используются предприятием для выпуска n видов продукции. Известна экономическая выгода производства каждого вида продукции, исчисляемая, например, ценой реализации С = (С₁, С₂, … , С_n). Известны технологические коэффициенты а_ij, соответствующие количеству i-го вида ресурса, необходимого для производства единицы j –го вида продукции – А = ( а_ij ). Необходимо составить план производства х = (х₁,х₂, … , х_n), приносящий предприятию максимальную прибыль.

В общем виде математическую модель задачи (ЗЛП) можно записать следующим образом:

F(x) = C₁x₁ + C₂x₂ + … + C_nx_n → max

a₁₁x₁ + a₁₂x₂ + … + a_1nx_n ≤ b₁, x_j ≥ 0, j=

a₂₁x₁ + a₂₂x₂ + … + a_2nx_n ≤ b₂,

… … … …

a_m1x₁ + a_m2x₂ + … + a_mnx_n ≤ b_m.

Рассмотрим задачу о диете. Необходимо составить диету (рацион), содержащую определенные питательные вещества. Имеем n видов продуктов, каждый из которых сожержит необходимые m видов питательных веществ. Единица j-го продукта содержит а_ij единиц i-го питательного вещества. Для нормальной жизнедеятельности необходимо не менее b_i единиц i-го вещества. Известна стоимость единицы каждого вида продукта С = (С₁, С₂, … , С_n). Необходимо составить диету минимальной стоимости.

Математическая модель задачи примет вид:

F(x) = C₁x₁ + C₂x₂ + … + C_nx_n → min

a₁₁x₁ + a₁₂x₂ + … + a_1nx_n ≥ b₁, x_j ≥ 0, j=

a₂₁x₁ + a₂₂x₂ + … + a_2nx_n ≥ b₂,

… … … …

a_m1x₁ + a_m2x₂ + … + a_mnx_n ≥ b_m.

Здесь х_j – количество j – го продукта в рационе.

 

В матричной форме общая ЗЛП выглядит так:

F(x) = C^Tx → max (min)

Ax ≤ (=,≥) B ; x ≥ 0.

Кроме того, для записи ЗЛП можно использовать знак суммы:

F(x) = → max (min)

, .

Рассмотрим задачу о размещении заказа. Имеется m однородных групп оборудования, на котором нужно выполнить заказ на выпуск n видов продукции в объемах х*_j, . Мощность оборудования ограничена, например, временем Т_i. Производительность оборудования задана коэффициентами а_ij. Известны коэффициенты затрат С_ij – затраты i – го оборудования на производство j – го продукта. Построить план х_ij размещения заказа (загрузки оборудования). Составим математическую модель задачи.

F(x) = 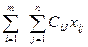→ min , x_ij ≥ 0, j= , ,

- по мощности - , ,

- по видам продукции, план по которой может быть перевыполнен

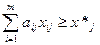, j= ,

- по видам продукции, план по которой должен соответствовать заказу

, j= ,

 

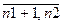- по видам продукции, заказ на которую принимается для более полной загрузки

оборудования

, j= .