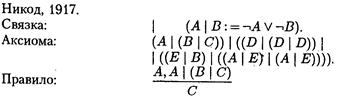Доказательство некоторых законов алгебры логики.

Лекция 6

Доказательство 4 и 5 пункта выполнить самостоятельно.

Правило снятия двойного отрицания.

Правило контрпозиции.

 

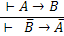
а) Если доказуема формула 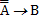, то доказуема формула A®B .

б) Если доказуема формула 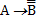. то доказуема формула А ®В .

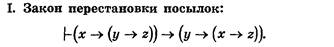
Из закона перестановки посылок вытекает правило перестановки посылок , которое применяется при выводе заключения:

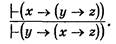
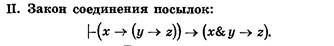
На практике в большей мере используется правило перестановки посылок:

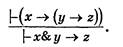
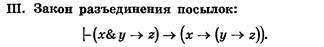
Правило разъединения посылок имеет вид:

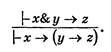
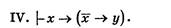
Доказательство. Сделаем подстановки в аксиомы I1 и IV 1

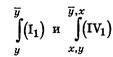
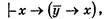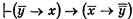В результате получим доказуемые формулы (1) и (2).

Из формул (1) и (2) по ПС следует

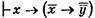
Применяя к этой формуле правило соединения посылок получим: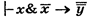

Используя ПСДО , получим .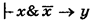

Применяя правило разъединения посылок получаем формулу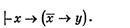

V. Закон исключенного третьего :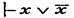

Доказательство. Воспользуемся доказуемой формулой 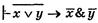(3)

Сделав в ней подстановку 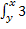, получим доказуемую формулу 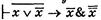(5)

В формуле (4) 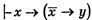сделаем подстановку: x заменим `x на , y на `y.

В результате получим формулу: 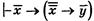. Применяя к ней правило соединения посылок, получим:

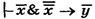.(6). Из (5) и (6) по ПС получаем 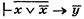, применяя ПК к данной формуле получим: .

По ПСДО .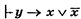

Подставив вместо y любую доказуемую формулу и применяя правило подстановки получим .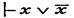

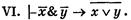Доказать самостоятельно.

Другие аксиоматизации исчисления высказываний

Рассмотренная теория не является единственной возможной аксиоматизацией исчисления высказываний.

Известны и многие другие аксиоматизации исчисления высказываний, предложенные различными авторами.

3.