Стационарных систем
АНАЛИЗ устойчивости линейных непрерывных
5.1 понятие об устойчивости линейной стационарной системы,
необходимое и достаточное условие устойчивости
основы теории устойчивости движения любых динамических систем, поведение которых описывается обыкновенными дифференциальными уравнениями, были разработаны великим русским ученым академиком А.М.Ляпуновым в 1892 г. в работе «Общая задача об устойчивости движения». Сущность определения устойчивости движения по А.М.Ляпунову состоит в следующем: невозмущенное движение системы называется устойчивым, если при всех t>t0 отклонение возмущенного движения от невозмущенного сколь угодно мало при достаточно малых начальных возмущениях в момент t0; невозмущенное движение системы называется асимптотически устойчивым, если отклонение возмущенного движения от невозмущенного стремится к нулю при t → ∞.
В теории управления за невозмущенное движение линейной стационарной САУ обычно принимают установившееся состояние (установившийся статистический или динамический режим), а за возмущенное – неустановившееся движение, т.е. переходный процесс. При этом для линейных стационарных САУ практическое значение имеет асимптотическая устойчивость. Поэтому, в соответствии с понятием устойчивости по А.М.Ляпунову, линейная стационарная САУ называется асимптотически устойчивой, если она обладает свойством возвращаться с течением времени в исходное установившееся состояние после прекращения действия тех возмущений, которые вывели ее из этого состояния. Иначе говоря, асимптотическая устойчивость (в дальнейшем для краткости слово «асимптотическая» будем опускать) линейных стационарных систем связана с их собственным движением. Математически это движение описывается выражением вида:
 , (5.1)
, (5.1)
в котором pi являются корнями характеристического уравнения замкнутой САУ
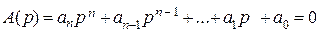 (5.2)
(5.2)
или характеристического уравнения разомкнутой системы
 (5.3)
(5.3)
ранее было показано, что если в характеристических уравнениях (5.2) и (5.3) все корни имеют отрицательные вещественные части, то
 (5.4)
(5.4)
и система будет устойчива.
Следовательно, необходимым и достаточным условием устойчивости линейной (линеаризованной) стационарной системы является отрицательность вещественных частей всех корней ее характеристического уравнения. Наличие в характеристическом уравнении хотя бы одного корня с положительной вещественной частью означает, что система неустойчива. Если среди корней характеристического уравнения имеется пара чисто мнимых корней или один нулевой корень, а вещественные части всех остальных корней отрицательны, то система находится на колебательной или апериодической границе устойчивости. В характеристическом уравнении (5.2) наличие одного нулевого корня возможно лишь при условии a0 = 0. однако в физически реализуемых системах характеристический многочлен А(р) является полным многочленом: в статистических САУ (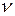 = 0) a0 = 1 + К, а в статистических САУ (
= 0) a0 = 1 + К, а в статистических САУ (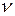 ≠ 0, т.е.
≠ 0, т.е. 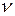 = 1,
= 1, 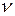 = 2, …) a0 = К. А это означает, что замкнутая САУ может находится только на колебательной границе устойчивости.
= 2, …) a0 = К. А это означает, что замкнутая САУ может находится только на колебательной границе устойчивости.
В отличие от характеристического уравнения (5.2) замкнутой САУ, характеристическое уравнение (5.3) разомкнутой системы может содержать как чисто мнимый, так и нулевой корень, т.е. разомкнутая система может находиться как на колебательной, так и на апериодической границе устойчивости.
5.2 Теоремы А.М.Ляпунова об устойчивости.
Критерии устойчивости
Теоретическим обоснованием законности исследования устойчивости реальных систем по их линеаризованным уравнениям, которые представляют собой уравнения первого приближения, служат теоремы, доказанные А.М.Ляпуновым.
ТЕОРЕМА 1. Если вещественные части всех корней характеристического уравнения первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво, независимо от членов разложения выше первого порядка малости.
ТЕОРЕМА 2. Если среди корней характеристического уравнения первого приближения найдется, по меньшей мере, один корень с положительной вещественной частью, то невозмущенное движение асимптотически неустойчиво, независимо от членов разложения выше первого порядка малости.
А.М.Ляпунов исследовал также критические случаи, когда среди корней характеристического уравнения первого приближения имеется один нулевой корень или одна пара чисто мнимых корней, а вещественные части всех остальных корней отрицательные. Он доказал, что в этих случаях вопрос об устойчивости движения реальной системы может быть решен лишь с учетом членов разложения второго и более высокого порядка малости, т.е. на основании дополнительных исследований по исходным нелинейным уравнениям (теорема 3). Однако, на практике часто принимают, что если линеаризованная система находится на границе устойчивости, то и исходная система тоже находится на границе устойчивости. Объясняется это тем, что САУ, которая используется на практике, должна быть не только устойчивой, но и иметь определенный запас устойчивости. иначе говоря, она должна находится на некотором расстоянии от границы устойчивости. В противном случае при незначительном изменении того или иного параметра (или совокупности параметров) система может стать неустойчивой. Поэтому узкая зона, переход которой переводит линеаризованную систему из устойчивого состояния в неустойчивое, включает в себя также границу устойчивости исходной реальной системы. Значение параметра (параметро), при котором система находится на границе устойчивости, называется критическим значением.
В теории автоматического управления для наглядности иллюстрации необходимого и достаточного условия устойчивости часто прибегают к комплексной плоскости корней и судят об устойчивости САУ по расположению корней характеристического уравнения (полюсов передаточной функции) в этой плоскости. На рис. 5.1 показан пример возможного расположения корней в виде точек на комплексной плоскости (α; jω) для системы, описываемой уравнением пятого порядка. Из рис. 5.1а следует, что для устойчивости линейной стационарной системы необходимо и достаточно, чтобы все корни ее характеристического уравнения лежали в левой полуплоскости комплексной плоскости корней, т.е. чтобы все корни были левыми. Если хотя бы один корень находится справа от мнимой оси, т.е. является правым, то САУ неустойчива (рис. 5.1б). в случае если один корень располагается на мнимой оси, а остальные корни левые, то система будет находиться либо на апериодической (рис. 5.1в), либо на колебательной (рис. 5.1г) границе устойчивости. Следовательно, мнимую ось плоскости корней можно рассматривать как границу устойчивости.
 |
Рисунок 5.1
Таким образом, естественным методом исследования устойчивости САУ является нахождение корней характеристического уравнения и определение знаков их вещественных частей. Однако такой метод не может считаться приемлемым для большинства практических задач. Это связано с математическими трудностями, возникающими при вычислении корней характеристического уравнения третьей и более высокой степени. Кроме того, найдя корни характеристического уравнения и определив, устойчива или неустойчива система, мы не сможем установить, как те или иные параметры влияют на устойчивость и, следовательно, представить себе, как нужно изменить параметры системы или ее структуру для обеспечения устойчивости. Поэтому в инженерной практике широкое применение получили косвенные методы исследования САУ на устойчивость, называемые критериями устойчивости.
Критерий устойчивости – это математически сформулированные правила, позволяющие исследовать устойчивость системы без вычисления корней характеристического уравнения. Они подразделяются на алгебраические и частотные. К алгебраическим относятся критерии Вышнеградского, Рауса, Гурвица и др. Частотными являются критерии Михайлова и Найквиста. С математической точки зрения все критерии устойчивости эквивалентны друг другу, так как они устанавливают факт отрицательности или положительности вещественных частей корней характеристического уравнения. Целесообразность применения того или иного критерия определяется исходными данными, характером задачи исследования, а также имеющимися вычислительными средствами.
Следует заметить, что простейшим критерием является необходимое условие устойчивости: для устойчивости САУ необходимо, чтобы все коэффициенты характеристического уравнения были положительными. Этот вывод вытекает из теоремы Безу, согласно которой характеристическое уравнение можно представить в виде:

Если все корни р1, р2, … рn будут иметь отрицательные действительные части, то все коэффициенты в характеристическом уравнении будут положительными. (для вещественных корней это очевидно, для комплексных – проверьте самостоятельно).
5.3 Критерий устойчивости Гурвица
в 1895 г. немецким математиком А.Гурвицом были выведены аналитические условия отрицательности вещественных частей всех корней характеристического уравнения n-й степени в виде системы неравенств, содержащих коэффициенты этого уравнения. в теории автоматического управления эти условия известны под названием критерия устойчивости Гурвица.
по критерию Гурвица можно судить об устойчивости систем как в замкнутом, так и в разомкнутом состоянии. Для этого необходимо воспользоваться в первом случае характеристическим уравнением (5.2), а во втором случае – характеристическим уравнением (5.3).
Рассмотрим критерии Гурвица включает применительно к замкнутой САУ с характеристическим уравнением:
 (5.5)
(5.5)
и приведем его формулировку без доказательства.
Математической основой критерия является теория определителей. Система неравенства Гурвица включает в себя главный определитель ∆n Гурвица и все его диагональные миноры ∆i, где i = 1, 2, … , n-1.
Определитель ∆n составляется из коэффициентов характеристического уравнения (5.5) и имеет следующий вид:
    
| 1 | 2 | 3 | n-2 | n-1 | |||||||
| an-1 | an | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | 0 | ||
| an-3 | an-2 | an-1 | an | 0 | 0 | 0 | … | 0 | 0 | 0 | ||
| an-5 | an-4 | an-3 | an-2 | an-1 | an | 0 | … | 0 | 0 | 0 | ||
| ∆n = | . | . | . | . | . | . | . | . | . | . | . | (5.6) |
| . | . | . | . | . | . | . | . | . | . | . | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | a2 | a3 | a4 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | a0 | a1 | a2 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | a0 |
Правило составления следующее. По главной диагонали записывают все коэффициенты уравнения (5.5), начиная с an-1 до a0 включительно в порядке нумерации. Затем заполняют горизонтальные строки: справа от каждого элемента главной диагонали записывают коэффициенты с последовательно возрастающими индексами, а слева – с последовательно убывающими индексами. При этом вместо коэффициентов с индексами, большими n или меньшими 0, записывают нули (в случае отсутствия в характеристическом уравнения какого-либо коэффициента также записывается нуль).
Диагональные миноры ∆i, где i = 1, 2, …, (n-1), представляют собой определители Гурвица низшего порядка. Они получаются отчеркиванием i-й строки и i-го столбца, как это показано в ∆n штриховыми линиями и имеют вид:
| ∆1 = an-1; | ∆2 = | an-1 | an | ; … | ∆n = ∆n-1 a0; |
| an-3 | an-2 |
Формулировка критерия: для устойчивости системы с характеристическим уравнением

необходимо и достаточно, чтобы при an > 0 главный определитель Гурвица и все его диагональные миноры были положительны, т.е. чтобы
an > 0; ∆1 > 0; ∆2 > 0; … ∆n-1 > 0; ∆n > 0 (5.7)
Гурвиц показал, что если an > 0; ∆1 > 0; ∆2 > 0; … ∆n-2 > 0, а ∆n = ∆n-1a0 = 0, т.е. a0 = 0 при ∆n-1 > 0 или ∆n-1 = 0 при a0 > 0, то характеристическое уравнение (5.5) будет иметь один нулевой корень или одну пару чисто мнимых корней. При этом все остальные корни будут левыми. Это означает, что в первом случае система будет находиться на апериодической границе устойчивости, а во втором случае – на колебательной границе устойчивости. Причем, первый случай может иметь место только в разомкнутой системе, а второй – как в разомкнутой, так и в замкнутой. Таким образом, выражение ∆n-1 = 0 является условием нахождения замкнутой САУ на колебательной границе устойчивости. Воспользовавшись равенством ∆n-1 = 0, можно при заданных параметрах системы принять за неизвестный какой-либо из них (например, коэффициент усиления) и определить его критическое значение.
Найдем условия устойчивости по Гурвицу для замкнутых САУ первого, второго, третьего и четвертого порядков, т.е. для систем с характеристическим уравнением  , когда n = 1, n = 2, n = 3, n = 4.
, когда n = 1, n = 2, n = 3, n = 4.
САУ первого порядка.
Характеристическое уравнение: 
Главный определитель Гурвица: ∆n = ∆1 = | a0 | = a0
Необходимое и достаточное условие устойчивости по критерию Гурвица: a1 > 0; a0 > 0.
САУ второго порядка.
Характеристическое уравнение: 
Главный определитель Гурвица ∆n = ∆2 и его диагональный минор ∆1:
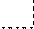 ∆n = ∆2 = ∆n = ∆2 =
| a1 | a2 | = a1a0; | ∆1 = a1 |
| 0 | a0 |
Согласно критерию Гурвица: a2 > 0; ∆1 = a1 > 0 и ∆2 = a1a0 > 0, т.е. при a1 > 0, a0 > 0, то САУ устойчива. Следовательно, для САУ второго порядка необходимое и достаточное условие устойчивости имеет вид:
a2 > 0; a1 > 0; a0 > 0
Равенство ; ∆1 = a1 > 0 при a2 > 0 и a0 > 0 является условием нахождения системы на колебательной границе устойчивости.
САУ третьего порядка.
Характеристическое уравнение: 
Главный определитель Гурвица ∆n = ∆3 и его диагональный минор ∆1 и ∆2 имеют вид:
  ∆n = ∆n =
| a2 | a3 | 0 | ; ∆1 = a2; | ∆1 = | a2 | a3 | = a1a2 - a0a3 |
| a0 | a1 | a2 | a0 | a1 | ||||
| 0 | 0 | a0 |
Согласно критерию Гурвица, если a3 > 0; ∆1 = a2 > 0, ∆2 = a2 a1 – a0 a3 > 0, ∆3 = ∆2a0 > 0, т.е. при ∆3 = (a2a1 – a0a3)a0 > 0, то САУ устойчива. Из неравенства ∆3 = ∆2a0 > 0 следует, что при a3 > 0, a2 > 0 и a0 > 0 определить ∆2 будет больше нуля, если, во-первых, a2a1 > 0, т.е. a1 > 0, и, во-вторых, a2a1 > a0a3. следовательно, для устойчивости САУ третьего порядка необходимо и достаточно, чтобы
a3 > 0, a2 > 0, a1 > 0, a0 > 0 и
a2a1 > a0a3, т.е. ∆2 > 0
если при a3 > 0, a2 > 0, a1 > 0, a0 > 0, ∆2 = a1a2 - a0a3 = 0, то САУ находится на колебательной границе устойчивости. При этом из равенства a1a2 - a0a3 = 0 находят критическое значение параметра.
Аналогично можно показать, что для устойчивости САУ четвертого порядка с характеристическим уравнением
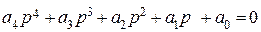
необходимо и достаточно, чтобы
a4 > 0, a3 > 0, a2 > 0, a1 > 0, a0 > 0 и
∆3 > 0
если при a4 > 0, …, a0 > 0, то САУ находится на колебательной границе устойчивости.
Таким образом, необходимым и достаточным условием устойчивости по Гурвицу для САУ первого и второго порядков является положительность коэффициентов характеристического уравнения, а для САУ третьего и четвертого порядков – положительность коэффициентов характеристи-ческого уравнения и выполнение дополнительных неравенств ∆2 > 0 и ∆3 > 0 соответственно.
Для систем пятого и шестого порядков кроме положительности коэффициентов характеристического уравнения, требуется выполнение неравенств ∆2 > 0, ∆4 > 0 и ∆3 > 0, ∆5 > 0 соответственно. следовательно, для систем выше четвертого порядка число дополнительных неравенств возрастает. Возрастает и сложность этих неравенств, практическое вычисление которых становится трудоемким. Поэтому критерий Гурвица целесообразно применять для систем не выше четвертого порядка (n ≤ 4).
5.4 Критерий устойчивости Михайлова
критерий устойчивости Михайлова относится к так называемым частотным критериям, которые основаны на использовании частотных характеристик САУ. Они позволяют сравнительно просто получить ответ об устойчивости системы, дают возможность судить о влиянии на устойчивость САУ различных ее звеньев, позволяют исследовать устойчивость таких САУ, у которых неизвестны уравнения связи отдельных элементов, но имеется возможность экспериментального определения частотных характеристик.
В 1938 году А.В.Михайлов предложил графо-аналитический критерий устойчивости, применяемый для определения устойчивости замкнутых автоматических систем любого порядка.
Применение критерия устойчивости Михайлова связано с построением характеристической кривой, которая называется также кривой Михайлова, описываемой характеристическим вектором на комплексной плоскости.
Характеристический вектор замкнутой системы получают из характеристического многочлена.
 (5.8)
(5.8)
путем замены р на јω.
Сделав замену и произведя группировку членов, содержащих и не содержащих ј, получим

(5.9)
где  – вещественная часть вектора;
– вещественная часть вектора;
 – мнимая часть вектора.
– мнимая часть вектора.
Задаваясь различными значениями ω от 0 до ∞ и откладывая Х(ω) по оси абсцисс, а У(ω) – по оси ординат декартовой системы координат, строят кривую, называемую годографом характеристического вектора или годографом Михайлова. Анализируя выражение (5.9), нетрудно заметить, что:
1) при ω = 0 этот годограф начинается в точке a0, лежащей на вещественной оси, а заканчивается в точке, соответствующей ω = ∞. Эта точка лежит в n-м квадранте, где n – степень характеристического полинома (5.8);
2) кривая Михайлова симметрична относительно вещественной оси, что следует из четности Х(ω) и нечетности функции У(ω). Поэтому при исследовании систем кривая строится только для положительных значений частоты ω (0 ≤ ω ≤ ∞);
3) в устойчивой системе края Михайлова при изменении ω от 0 до ∞ последовательно обходит все квадранты против часовой стрелки, охватывая начало координат.
Формулировка критерия.
Для устойчивости замкнутой САУ необходимо и достаточно, чтобы кривая Михайлова при изменении частоты ω от 0 до ∞ обходила последовательно в положительном направлении (против хода часовой стрелки) n квадрантов комплексной плоскости, где n – степень характеристического многочлена.
Если годограф проходит через начало координат, то система находится на границе устойчивости.
Кривые Михайлова для устойчивых систем различного порядка изображены на рис. 5.2.

Рисунок 5.2
Рисунок 5.3
Рисунок 5.4
Кривые Михайлова, соответствующие неустойчивым САУ, изображены на рис. 5.3.
На рис. 5.3 видно, что здесь нарушена очередность пересечения кривыми осей координат (или порядок обхода маршрутов).
Для системы, находящейся на границе устойчивости, кривая Михайлова изображена на рис. 5.4. она проходит через начало координат. В этом случае при ω = ωк выполняется равенство Х(ωк) = 0, У(ωк) = 0. одно из этих равенств позволяет найти частоту колебаний ωк, а другое – критическое значение какого-либо параметра (например, К).
Таким образом, чтобы оценить устойчивость замкнутой САУ с помощью критерия Михайлова, необходимо:
1. Найти А(р) = В(р) + D(р).
2. Подставить р = јω в А(р), получить А(јω) и выделить Х(ω) и У(ω), т.е. А(јω) = Х(ω) + јУ(ω).
3. построить по нескольким значениям Х(ω1) и У(ω1) А(јω).
4. Воспользоваться формулировкой и оценить устойчивость.
5.5 Критерий устойчивости Найквиста
в 1932 году американским ученым Найквистом был предложен частотный критерий для исследования усилителей с отрицательной обратной связью (т.е. для замкнутых автоматических систем). этот критерий обобщил и в 1938 году впервые применил в теории автоматического регулирования А.В.Михайлов. в связи с этим этот критерий часто называют критерием Михайлова-Найквиста.
Частотный критерий Найквиста отличается тем, что он позволяет судить об устойчивости замкнутых систем по амплитудно-фазовой характеристике разомкнутой системы W(јω) (рис. 5.5)
АФХ строится по

при р = јω. Примерный вид АФХ для статистической системы представлен на рис. 5.5а, для астатической – на рис. 5.5б.
прежде чем приступить непосредственно к изучению критерия Найквиста, сделаем ряд предварительных замечаний.
1. для анализа устойчивости ЗСАУ по критерию Найквиста необходимо знать количество корней с положительной вещественной частью в характеристическом уравнении РСАУ, т.е. количество правых корней.
 |
Рисунок 5.5
Пример 1
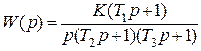
Характеристическое уравнение РСАУ

имеет корни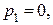

 , т.е. количество правых корней l = 0.
, т.е. количество правых корней l = 0.
Пример 2

 ;
; 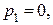


т.е. имеет один правый корень (l = 1).
Пример 3

 ;
; 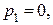

 , т.е. l = 2.
, т.е. l = 2.
При l = 0 в соответствии с необходимым и достаточным условием устойчивости РСАУ является устойчивой, при l ≠ 0 – неустойчивой.
2. На комплексной плоскости выделяют критическую точку с координатами [-1; ј0] (см. рис. 5.6).
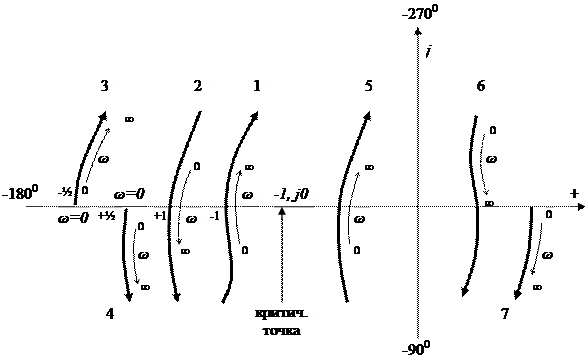 |
Рисунок 5.6
кроме того, вводят понятие отрицательных и положительных переходов АФК через отрезок вещественной оси [-∞; -1] (рис. 5.6). Если при увеличении ω ФЧХ Ө(ω) уменьшается, то переход является отрицательным -1, (кривая 1); если же Ө(ω) увеличивается – положительным +1 (кривая 2). В случае, если АФХ начинается на отрезке [-∞; -1], то считают, что имеется половина перехода: отрицательного -½ (кривая 3) или положительного +½ (кривая 4). Переходы АФХ через отрезок вещественной оси [-1; +∞] не учитываются (кривые 5, 6, 7).
3. При оценке устойчивости астатических систем на АФХ необходимо дополнить при ω = 0 другой бесконечно большого радиуса от вещественной оси (рис. 5.7)
Правила дополнения:
а) при l четном (и l = 0) АФХ дополняется дугой от положительной вещественной полуоси;
б) при l нечетном АФХ дополняется дугой от отрицательной вещественной полуоси.

Рисунок 5.7
Перейдем к рассмотрению критерия Найквиста.
Формулировка критерия Найквиста.
Для устойчивости замкнутой САУ необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов АФХ разомкнутой САУ через отрезок вещественной оси [-∞; -1] была равна  , где l – число правых корней характеристического уравнения разомкнутой системы.
, где l – число правых корней характеристического уравнения разомкнутой системы.
Рассмотрим применение критерия Найквиста для систем, устойчивых и неустойчивых в разомкнутом состоянии.
1. Системы, устойчивые в разомкнутом состоянии (l = 0).
Пример 1.
 – система статическая (ν = 0)
– система статическая (ν = 0)
Количество правых корней l = 0 (

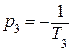 ). Вид АФХ при различных значениях коэффициента передачи представлен на рис. 5.8.
). Вид АФХ при различных значениях коэффициента передачи представлен на рис. 5.8.
Так как l = 0, то для устойчивости данной САУ в замкнутом состоянии необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов через отрезок [-∞; -1] была равна нулю.
В нашем случае:
а) для кривой 1: положительных переходов – ноль, отрицательных – ноль, разность ∆ = 0, следовательно, САУ при К = К1 будет устойчивой;

Рисунок 5.8
б) для кривой 2: положительных переходов – ноль, отрицательных – один, разность ∆ = 0 - 1 = -1 ≠ 0, следовательно, САУ при К = К2 будет неустойчивой;
в) при К = Ккр система находится на границе устойчивости.
Пример 2.
 – система Астатическая (ν = 1)
– система Астатическая (ν = 1)
Количество правых корней l = 0 (р1 = 0; 
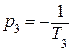 ). Вид АФХ с дополнительными дугами для различных значений коэффициента передачи показан на рис. 5.9 (дополнение проведено от положительной полуоси, т.к. l =0 – четное).
). Вид АФХ с дополнительными дугами для различных значений коэффициента передачи показан на рис. 5.9 (дополнение проведено от положительной полуоси, т.к. l =0 – четное).
Анализ устойчивости данной системы аналогичен предыдущему случаю, т.е. при АФХ вида 1 – замкнутая САУ устойчива; 2 – неустойчива; 3 – находится на границе устойчивости.
Анализ рис. 5.8 и 5.9 показывает, что для САУ, устойчивых в разомкнутом состоянии (l = 0) критерий Найквиста можно сформулировать следующим образом:
Для устойчивости замкнутой САУ, устойчивой в разомкнутом состоянии, необходимо и достаточно, чтобы АФХ разомкнутой САУ не охватывала точку [-1; ј0].
2. Системы, неустойчивые в разомкнутом состоянии (l ≠ 0).
 |
Рисунок 5.9
Пример 1.
 – система статическая (ν = 1)
– система статическая (ν = 1)
Количество правых корней l = 1 (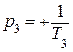 ).
).
 Вид АФХ при различном соотношении постоянных времени представлен на рис. 5.10.
Вид АФХ при различном соотношении постоянных времени представлен на рис. 5.10.
Рисунок 5.10
Так как l = 1, то для устойчивости данной САУ в замкнутом состоянии необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов через отрезок [-∞; -1] была равна  = ½.
= ½.
В нашем случае:
а) для кривой 1: положительных переходов ½, отрицательных – ноль, разность ∆ = ½ - 0 = ½ =  , т.е. необходимое и достаточное условие выполняется, следовательно, САУ с АФХ вида 1 в замкнутом состоянии будет устойчива;
, т.е. необходимое и достаточное условие выполняется, следовательно, САУ с АФХ вида 1 в замкнутом состоянии будет устойчива;
б) для кривой 2: положительных переходов ½, отрицательных – 1, разность ∆ = ½ -1 = - ½ ≠  , следовательно, САУ неустойчива в замкнутом состоянии;
, следовательно, САУ неустойчива в замкнутом состоянии;
в) система, имеющая АФХ вида 3, находится на границе устойчивости.
Пример 2
 – система Астатическая (ν = 1)
– система Астатическая (ν = 1)
Количество правых корней l = 1 (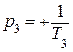 ). Вид АФХ с дополняющей дугой приведен на рис. 5.11 (дополнение проведено от отрицательной полуоси, так как l = 1 – нечетное).
). Вид АФХ с дополняющей дугой приведен на рис. 5.11 (дополнение проведено от отрицательной полуоси, так как l = 1 – нечетное).
Для устойчивости данной САУ необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов через отрезок [-∞; -1] была равна  = ½.
= ½.
рисунок 5.11 | В нашем случае: положительных – ноль, отрицательных – ½, разность ∆ = 0 - ½ = - ½ ≠ ½, следовательно, данная САУ в замкнутом состоянии неустойчива, причем ее устойчивость не достигается никаким изменением параметров.
Таким образом, для оценки устойчивости замкнутой САУ по критерию Найквиста необходимо:
1. получить передаточную функцию разомкнутой САУ 
|
2. Определить, устойчива ли разомкнутая САУ и выяснить количество правых корней l в D(р) = 0.
3. Построить АФХ W(јω).
4. Подсчитать разность ∆ между числом положительных и отрицательных переходов АФХ через отрезок [-∞; -1].
5. Сравнить значения ∆ и  .
.
6. Сделать заключение об устойчивости САУ в замкнутом состоянии.
В том случае, если САУ в разомкнутом состоянии устойчива (l = 0), можно применять формулировку, основанную на охвате точки [-1; ј0], не считая переходов.
Следует заметить, что в случае нахождения САУ на границе устойчивости для частоты ω = ωк (соответствующей точке [-1; ј0]), справедлива система уравнений



Решая данную систему, находят значения частоты незатухающих колебаний ωк и критическое значение коэффициента передачи системы Ккр.
5.6 Анализ устойчивости системы по ЛЧХ
известно, что ЛЧХ L(ω) и Ө(ω) однозначно связаны с АФХ W(jω):
L(ω) = 20lq| W(јω)|; Ө(ω) = arq W(јω)
Отсюда следует, что формулировки критерия Найквиста применительно к ЛЧХ L(ω), Ө(ω) можно получить из сопоставления АФХ W(јω) с соответствующими ей ЛЧХ L(ω) и Ө(ω).
На рис. 5.12 и 5.13 приведены АФХ и соответствующие им ЛЧХ для системы устойчивой (l = 0) (рис. 5.12) и неустойчивой (l = 1) (рис. 5.13) в разомкнутом состоянии.
При оценке устойчивости нас интересует число переходов АФХ через отрезок [-∞; -1]. Чем он характерен?
1. На этом отрезке Н(ω) > 1, следовательно,
L(ω) = 20lqН(ω) > 0
2. Значение фазовой характеристики Ө(ω) на этом отрезке равно -1800.
Таким образом, переходам АФХ W(јω) через отрезок [-∞; -1] соответствуют переходы ЛФХ Ө(ω) через прямую -1800 в области частот, где ЛАХ L(ω) > 0. при этом дополнению АФХ астатических систем дугой бесконечно большого радиуса соответствует дополнение ЛФХ Ө(ω) при ω→0 монотонным участком, приводящим ЛФХ к прямой 00 (при l – четным) или -1800 (при l – нечетном) (см. рис. 5.14).
Формулировка критерия.
Для устойчивости замкнутой САУ необходимо и достаточно, чтобы в области частот, где ЛАХ положительна, разность между числом положительных и отрицательных переходов ЛФХ через прямую -1800 была равна l/2, где l – число правых корней характеристического уравнения разомкнутой САУ.
Исходя из формулировки критерия, при оценке устойчивости замкнутой САУ по ЛЧХ необходимо:
1. Получить передаточную функцию разомкнутой САУ.

2. Определить, устойчива ли разомкнутая САУ и выяснить количество правых корней l и D(р) = 0.
3. Построить ЛЧХ L(ω) и Ө(ω).
4. Выделить интервалы частот, где ЛАХ положительны, т.е. L(ω) > 0.
5. Подсчитать разность ∆ между числом положительных и отрицательных переходов ЛФХ через прямую -1800 в выделенном интервале частот.
6. Сравнить значения ∆ и l/2.
7. Сделать заключение об устойчивости САУ в замкнутом состоянии.
Применяя данную методику к ЛЧХ, изображенным на рис. 5.12, 5.13, 5.14 можно сделать вывод, что данные САУ устойчивы в замкнутом состоянии.
Для систем, устойчивых в разомкнутом состоянии (l = 0), иногда удобнее пользоваться следующей формулировкой:
Для устойчивости замкнутой САУ, устойчивой в разомкнутой состоянии, необходимо и достаточно, чтобы в области частот, где ЛАХ положительна, ЛФХ не опускалось ниже прямой -1800.
Пример.
Предположим, что система с передаточной функцией
 при К = К1 и К = К2
при К = К1 и К = К2
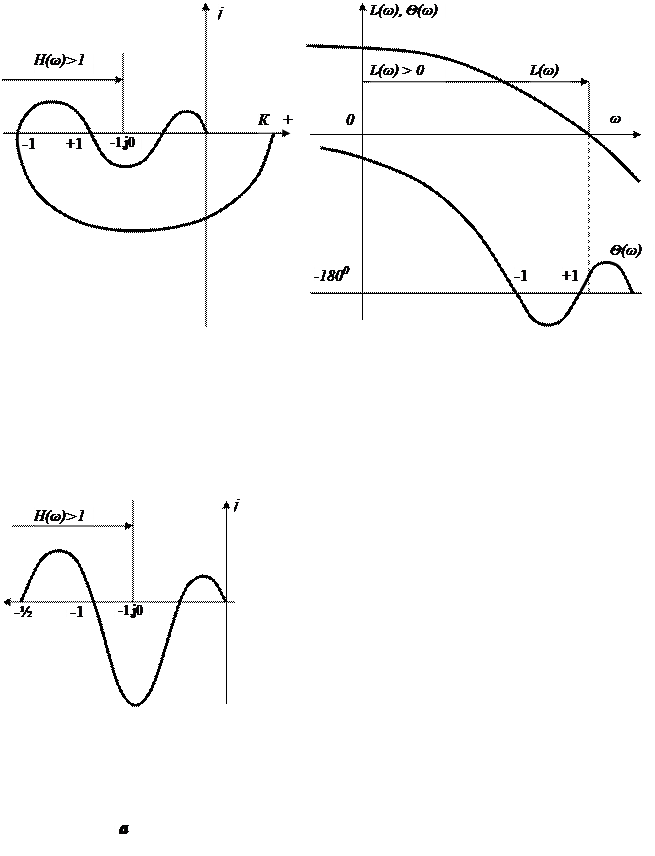

Рисунок 5.12
 |
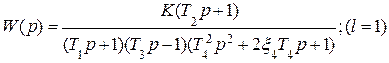
рисунок 5.13
 |

Рисунок 5.14
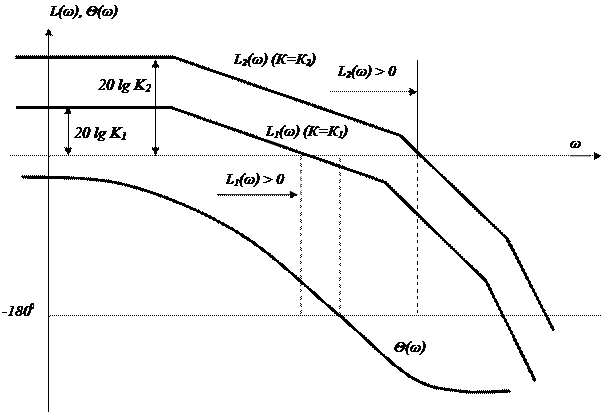 |
Рисунок 5.15
имеет ЛЧХ, изображенное на рис. 5.15. применение последней формулировки позволяет установить, что при К = К1 замкнутая САУ будет устойчива, при К = К2 – неустойчива. Аналогичные результаты могут быть получены и на основе общей формулировки.
5.7 Запас устойчивости
при проектировании систем автоматического управления всегда стремятся обеспечить их устойчивость так, чтобы изменение параметров в определенных пределах не могло привести к неустойчивости, т.е. всегда стремятся обеспечить их устойчивость с некоторой гарантией. Для этой цели используется понятие запаса устойчивости системы.
Запас устойчивости системы – это количественная характеристика степени удаления системы от границ устойчивости.
Наличие определенного запаса устойчивости гарантирует сохранение устойчивости системы при изменении ее параметров в определенных пределах. Чем больше запас устойчивости, тем меньше вероятность того, что система в процессе эксплуатации станет неустойчивой.
Запас устойчивости необходим еще и потому, что он определяет характер переходных процессов в системах. Наличие определенного запаса устойчивости обеспечивает работу реальной системы в области устойчивости с требуемым качеством переходного процесса.
При инженерных расчетах в качестве меры запаса устойчивости наиболее широко используют вытекающие из критерия Найквиста две величины: запас устойчивости по амплитуде (модулю) и запас устойчивости по фазе. оба эти запаса рассматриваются одновременно и определяются либо по АФХ W(јω), либо по соответствующим ей ЛЧХ L(ω), Ө(ω). В дальнейшем будем пользоваться следующими обозначениями: Н3 и L3 – запас устойчивости по амплитуде; Ө3 – запас устойчивости по фазе.
Для определения запасов устойчивости введем в рассмотрение две частоты (рис.5.16):
ωс – частота среза – частота, на которой АЧХ равна единице (или ЛАХ равна нулю), т.е.
Н(ωс) = 1; L(ωс) = 20lqН(ωс) = 0
ωπ – частота, на которой фазовая характеристика равна -1800, т.е. Ө(ωπ) = -1800.
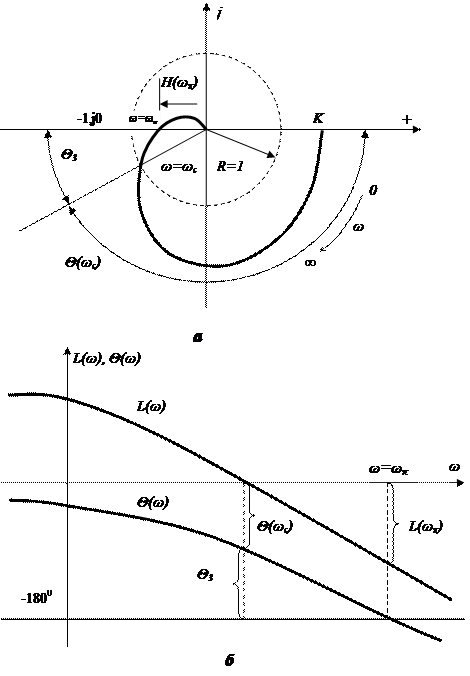 |
Рисунок 5.16
Под запасом устойчивости по амплитуде обычно понимается величина Н3 в относительных единицах или величина L3 в дБ, которая показывает, как нужно изменить коэффициент передачи системы при неизменных фазовых соотношениях, чтобы привести ее к границе устойчивости. Он определяется по формулам:
 ; Lз = 20lqНз = -20 lqН(ωπ) = -L(ωπ)
; Lз = 20lqНз = -20 lqН(ωπ) = -L(ωπ)
где – Н(ωπ) и L(ωπ) – значение АЧХ и ЛАХ на частоте ωπ (см. рис. 5.16).
под запасом устойчивости по фазе понимается величина угла в градусах, которая показывает на сколько должен возрасти отрицательный сдвиг по фазе (запаздывание по фазе) в системе на частоте среза при неизменном значении коэффициента усиления, чтобы система оказалась на границе устойчивости. Величина Ө3 определяется по АФХ и по ЛЧХ на основании формулы
Ө3 = 1800 - | Ө(ωс) |
где ωс – частота среза; | Ө(ωс) | - значение ФЧХ на частоте среза, взятое по модулю. Чем больше величина Ө3, тем больше запас устойчивости по фазе (см. рис. 5.16).
необходимые значения запасов устойчивости зависят от типа САУ и выбираются при проектировании систем, исходя из требований, предъявляемых к качеству переходного процесса. Ориентировочно должно быть Ө3 ≥ 300, L3 ≥ 6 дБ.
5.8 Структурная устойчивость системы.
Понятие об области устойчивости и ее границах.
Устойчивость линейных стационарных САУ зависит не только от значений параметров системы, но и от ее структуры. В связи с этим различают структурно устойчивые и структурно неустойчивые системы.
Система, устойчивость которой может быть обеспечена выбором ее параметров без изменения структуры, называется структурно устойчивой.
Система называется структурно неустойчивой, если невозможно обеспечить ее устойчивость не при каких значениях параметров. Структурно неустойчивую систему можно сделать устойчивой только путем изменения ее структуры. При проектировании системы это можно обеспечить, например, включением в управляющее устройство тех или иных корректирующих устройств.
Следовательно, структурно устойчивые системы, в отличие от структурно неустойчивых, имеют в пространстве некоторых своих параметров область их изменения, в которой система остается устойчивой. Эту область называют областью устойчивости. При исследовании и проектировании систем чаще всего возникает задача определения влияния одного или двух ее параметров на устойчивость, т.е. задача выделения области устойчивости на плоскости одного или двух параметров системы. Прежде чем приступить к решению этой задачи необходимо знать, имеет ли данная система область устойчивости или нет, т.е. является ли данная система структурно устойчивости или структурно неустойчивой.
Для построения границ области устойчивости можно использовать различные критерии устойчивости. Однако, чаще всего используется критерий Гурвица. При этом границы области устойчивости строится, исходя из условия:
∆n = a0 ∆n-1 = 0
обычно области устойчивости изображаются графически на плоскости двух параметров. Например, при исследовании системы управления ракет, вы встретитесь с областью устойчивости каналов автомата стабилизации на плоскости постоянных времени дифференцирующего контура.
