Свойства корреляционного момента

Свойство 1. .

Доказательство. .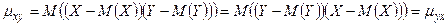

Свойство 2..

Доказательство. .

Свойство 3. Корреляционный момент двух независимых случайных величин Х и У равен нулю.

Доказательство. Так как Х и У независимые случайные величины, то их отклонения и также являются независимыми случайными величинами. Тогда, используя свойства математического ожидания, имеем право записать: .

Свойство 4. .

Доказательство. Используя свойства математического ожидания, имеем право записать:

Следствие.Для вычисления корреляционного момента дискретных и непрерывных случайных величин можно использовать соответственно формулы:

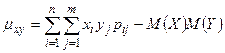и .

Определение 4. Нормированной случайной величиной относительно случайной величины Х называется случайная величина .

Замечание 6. Для нормированной случайной величины , .

Доказательство. Действительно ,

.

Свойство 5. .

Доказательство.Рассмотрим случайные величины Х и У, соответствующие им нормированные случайные величины и , и случайные величины . Очевидно, что случайные величины принимают только неотрицательные значения, следовательно, для их математических ожиданий справедливо неравенство:

, или

, по свойствам:

,

,

, или, учитывая замечание 6, , или , или .

Замечание 7.Таким образом, корреляционный момент служит для характеристики связи между величинами Х и У:

1) характеризует степень зависимости случайных величин Х и У;

2) характеризует разброс значений системы случайных величин .

Недостатком корреляционного момента является его зависимость от единиц измерения, т.е. значение корреляционного момента для одних и тех же случайных величин меняется в зависимости от того, в каких единицах эти величины измерены. Такая особенность затрудняет сравнение корреляционных моментов различных систем случайных величин.