Другие числовые характеристики

Определение 14. Модой дискретной случайной величиныХ называется её наиболее вероятное значение.

Замечание.Геометрически мода является абсциссой той точки полигона распределения, ордината которой максимальна.

Определение 15. Начальным моментом порядка случайной величины Х называется математическое ожидание величины : .

Замечание 1. В частности, , .

Замечание 2. Пользуясь определением моментов, дисперсию можно записать в виде .

Замечание 3. Начальные моменты позволяют учесть большие, но маловероятные значения случайной величины.

Определение 16. Центральным моментом порядка случайной величины Х называется математическое ожидание величины : .

Замечание 1.В частности .

Замечание 2. Нетрудно показать, что 1) , 2) ,

3) . Моменты более высоких порядков применяются редко.

Замечание 3. Рассмотренные моменты называют теоретическими.

Пример 1.Случайная величина Х имеет ряд распределения:


	0,4	0,2	0,1	0,3

Построить многоугольник распределения, найти функцию распределения вероятности и построить ее, найти математическое ожидание, дисперсию, СКО и моду случайной величины Х.

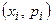Решение. 1) В прямоугольной системе координат отметим точки и соединим их последовательно ломаными отрезками. Получим многоугольник распределения (см. рис. 25.1).

2) Найдём функцию распределения вероятности.

Если , то .

Построим график функции распределения вероятности (см. рис. 25.2).

3) Найдём числовые характеристики случайной величины Х.

а) математическое ожидание: ;

б) дисперсия: ;

в) СКО: ;

г) мода случайной величины Х – это такое её значение, которому соответствует наибольшая вероятность; наибольшая вероятность соответствует значению ; поэтому .