Оценка погрешностей численного дифференцирования.

Также как и при интерполяции в численном дифференцировании возникают две погрешности: 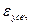и .

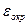Погрешность усечения – из-за замены функции на ее интерполирующий многочлен и ее производной на производную от интерполяционного многочлена.

Погрешность округления – из-за того, что значение функции в узлах x_i известны не точно, а с некоторой погрешностью h. Оценим погрешность усечения.

Теорема 5.1:

Погрешность усечения в формуле (5.3) численного дифференцирования (при суммировании k-слагаемых) имеет следующую оценку:

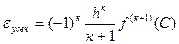
где С Î [х₀,х_к].

Доказательство:

Замечания:

При доказательстве теоремы был использован тот факт, что С=С(х) и С’(x) – существует. Это будет так, если функция f была достаточно гладкой.

Из-за того, что С’(x) мы вообще никак не можем оценить, погрешность усечения мы можем находить только в узлах интерполяции, с тем, чтобы 1-ое слагаемое, где присутствует С’(x), занулилось.

На практике формулу (5.8) мы заменяем на формулу (5.9) (оценка сверху для )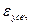

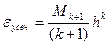(5.9)

где

Вспомним, что конечная разность очень похожа на производную ().

Тогда (5.9) можно заменить на (5.10):

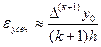
Для формул (5.5), (5.6) и (5.7) 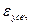можно вывести таким же образом, как и в теореме 5.1, получаем:

Для (5.5) ®

Для (5.6) ®

Для (5.7) →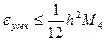

где ,

 

Оценим 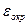для центральных формул.

Рассмотрим формулу (5.5)

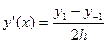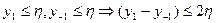, таким образом :

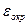Аналогично:

для (5.6) ®

для (5.7) ®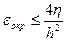

Заметим, что во всех формулах 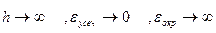при и при

Поэтому имеем следующую картину:

 

 

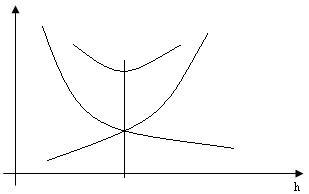
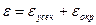
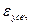
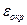
Таблица для погрешностей центральных формул:

4.6
4.7				15/8
4.8				2/