Обратная интерполяция.

П.5. Применение интерполяции.

С помощью обратной интерполяции можно решать нелинейные уравнения.

Решим f(x)=a:

Идея обратной интерполяции: пусть f в близи корня уравнения f(x)=a – монотонно возрастает или убывает, тогда у неё существует обратная функция.

g(x) – обратная функция, значение которой в точке а нас не интересует.

f(x)=a ;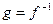

и будет искомым корнем уравнения f(x)=a,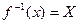

Возьмём интервал , на котором f – монотонна и имеет обратную функцию, следовательно, мы знаем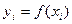

Применим интерполяцию для вычисления значений обратной функции g и найдем значение интерполирующей функции в точке а. Это и будет, приблизительно, искомый корень.

x=g(a)

При этом при интерполяции х и у меняются местами, так как мы интерполируем не f а g.

Пример:

х
у

f(x)=10

Решение находим интерполируя обратную функцию по 4-м точкам (например, по формуле Лагранжа).