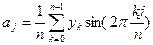П.4 Тригонометрическая интерполяция.

Поберей Л.С.

Краткий курс лекций. Часть II

Отпечатано в редакционно-издательском отделе Омского государственного промышленно-экономического колледжа

644029, г.Омск, ул. Нефтезаводская,6

1.В тригонометрической интерполяции в отличие от других видов интерполяции, интерполяция происходи не по , а по точкам, т.к. интерполирование происходит периодически и , т.е. период

2. , - равноотстоящие узлы интерполяции.

4.1.Формулы Т.И.:

(4.18а)

где , (4.18б)

Замечание:

в этих формулах i– мнимая единица и для работы по (4.18а) , (4.18б) нужна формула Эйлера: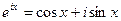

При Т.И. интерполирующая функция y(x):

1) периодична с периодом .

2) в узлах интерполяции , т.е. если -вещественное, то в узлах мнимая часть y – нулевая.

3) в промежуточных точках у может принимать комплексные значения, но Im y – будет не велика и её можно отбросить.

4) если число узлов интерполяции нечётное, т.е. n=2n+1, и все - вещественные, то функция у полученная по (4.18а) , (4.18б) сама по себе будет вещественна.

Коэффициенты - комплексные, а - вещественные функции и в этом случае вычисления можно осуществлять не с комплексными, а с вещественными числами по формуле (4.19).

(4.19а)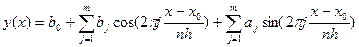

(4.19б) 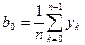; ;