Имитационное моделирование многокомпонентных систем
Сложные экономические системы, в которых можно выделить основные компоненты, проще всего изучать с помощью моделей многокомпонентных систем, основанных на применении ориентированных графов — орграфов.
При создании моделей сложных систем необходимо выявить и отобразить в моделях прямые и обратные связи, которые присутствуют в любой сложной системе. Благодаря наличию обратных связей в моделях результаты моделирования, анализа и прогноза оказываются гораздо более достоверными, чем при использовании структурных уравнений, в которых отражение этих обратных связей может вызвать большие затруднения. Наглядность и простота реализации аппарата решения многокомпонентных задач делает их доступными для широкого круга специалистов, не обладающих глубокими познаниями в области прикладной математики.
Геометрически ориентированный граф можно представить в виде набора вершин, обозначаемых кружками, и дуг, соединяющих эти вершины. Дуга задает направление от одной вершины к другой.
Путем в орграфе называется такая конечная последовательность дуг, в которой начало каждой последующей дуги совпадает с концом предыдущей. Дуги можно обозначить парой вершин, которые она соединяет. Например, от вершины 1 к вершине 2 ведут два пути: первый путь {(1.2)} и второй путь {(1.3); (3.2)}. Путь можно записать в виде последовательности вершин, через который он проходит. Например, второй путь можно записать следующим образом: {1,3, 2}.
Контуром называется путь, начальная вершина которого совпадает с конечной вершиной. На рис. 1 представлен орграф с контуром, проходящим через вершины 2, 4 и 3.
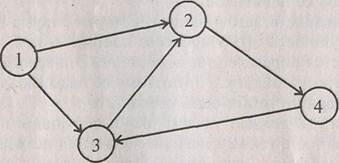
Рис. 1 - Пример орграфа с контуром
Вершины, в которые не заходят дуги, называются начальными. Вершины, из которых не выходит ни одна дуга, называются конечными.
Матрицей смежности вершин орграфа называется квадратная матрица, каждый элемент которой численно равен единице, если есть дуга, идущая от вершины i к вершине j. Если такой дуги нет, то элемент (if) матрицы смежности равен нулю. При решении многокомпонентных задач используются орграфы, в которых любые вершины i и j может непосредственно соединять только одна дуга. В табл. 1 показана матрица смежности для орграфа, представленного на рис. 1
Таблица 1-Таблица смежности орграфа
| Показатели i | Показатели j | |||
В качестве вершин используются показатели, а дуги указывают влияние изменения одного показателя на изменение другого. На рис. 2 представлен орграф, отражающий проблему состояния окружающей среды и развития промышленного центра.
Модель можно сделать более информативной, ее дугам орграфа приписать знак "плюс" или "минус". Знак "плюс" ставится в случае, если при увеличении значения показателя, от которого идет показатель, к которому дуга приходит, увеличивается. Знак "минус" ставится в обратном случае. Полученный орграф называется знаковым, на дугах знакового орграфа стоит +1 или —1, этот коэффициент можно обозначить еij. Эти коэффициенты образуют матрицу смежности, отличающуюся от приведенной выше матрицы наличием знаков ее элементов.
Моделирование ведется шагами, которые иногда называют импульсами. Сущность этого процесса состоит в том, что одной из вершин задается определенное изменение. Эта вершина актуализирует всю систему показателей, поэтому ее называют активизирующей. Таких вершин может быть несколько.
Исследователь должен указать активизирующие вершины, шаг изменений в них, а также начальные значения показателей во всех вершинах. Значения в вершинах будут меняться с каждым шагом имитации t, итог этого изменения определяется выражением
(pi)t = (рj)t-1 + Σij e ij · l ij · {(pi)t - (рj)t-1} (1)
где (pi)t и (рj)t-1 — величины показателей в вершине / при шагах
имитации соответственно t и (t — 1); еij и lij — коэффициенты, характеризующие знак и степень влияния показателя вершины i на показатель вершины j.
В этих моделях коэффициенты, характеризующие влияние смежных вершин кij, могут определяться на основе экспертных оценок или (если есть для этого данные) статистическими методами. Эти коэффициенты равны коэффициентам регрессионных линейных моделей, характеризующих связи показателей смежных вершин.
В модели могут вводиться лаги, то есть задержки передачи воздействия по каждой дуге во времени.
Рассматриваемым моделям присуща важная особенность. Это контур в формируемом орграфе, который обеспечивает моделирование обратной связи. Обратная связь является важнейшим элементом любой сложной экономической системы. Есть контуры, которые усиливают тенденцию к отклонению от начального состояния. Такие контуры называют контурами положительной обратной связи. Контуры, которые подавляют тенденцию к отклонению от начального состояния, называют контурами отрицательной обратной связи.
Контур модели является контуром положительной обратной связи, если содержит четное число дуг со знаком минус. В противном случае он является контуром отрицательной обратной связи.
Наличие в модели многих контуров, усиливающих отклонение, предполагает неустойчивость. В то же время наличие многих контуров, противодействующих отклонению, также может приводить к неустойчивости другого рода, которая проявляется в форме колебаний с увеличивающейся амплитудой. Если колебания показателей затухают и система приходит в определенное состояние, характеризующееся определенным уровнем показателей, то данная система устойчива.
Особенностью многокомпонентных задач является то, что с помощью орграфов удается объединить в модели системы различные социальные, экономические, экологические показатели. Часть из этих показателей может иметь статистическую базу, часть не иметь, часть может оцениваться количественно, а часть — качественно. С помощью решения многокомпонентных задач можно оценить тенденцию развития системы. При уточнении модели можно сформировать количественный прогноз изменения показателей системы, а также найти различные варианты воздействия на изучаемую систему с целью получения лучшего варианта.
Рассмотрим простейший пример, в котором используются временные задержки. На рис. 2 представлен орграф модели развития промышленного центра и состояния окружающей среды. В нем даны коэффициенты влияния — l и время задержки реализации воздействий — τ, в годах. В модели используются показатели в условных единицах.

Рис. 2 - Взвешенный орграф с временными задержками
для моделирования развития промышленного центра
и состояния окружающей среды
В результате моделирования на основе приведенного взвешенного орграфа с временными задержками можно получить тенденцию изменения показателей во времени. В частности, тенденцию числа рабочих мест, числа предприятий, численности населения и состояния окружающей среды. Таким образом, даже такая простейшая модель позволяет прогнозировать развитие довольно сложной системы.