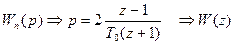Математические описания импульсных систем.

1. С помощью решетчатых функций.

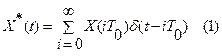i- номер интервала дискретности.

Х^*(t) – решетчатая функция.

Х(t) – огибающая решетчатой функции.

 

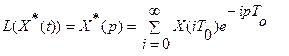- дискретное преобразование Лапласа.

Введем новую переменную Z=e^pTo Þ

Вводим Z-преобразование для дискретной системы

Преобразование непрерывного сигнала X(t) в дискретный сигнал X(z)

1). Х(t) ® Х^*(t) ® Х^*(p) ® Х(z )

Выбираем Т₀

Х(t)	X(p)	X(z)

2). По таблице преобразований Лапласа и Z-преобразований.

 

Свойства Z- преобразований.

1. Линейность – Z{ a₁X₁(t)+ a₂X₂(t)}= a₁X₁(z)+ a₁X₁(z)

2. Теореме о начальном значении оригинала

3. Теореме о конечном значении оригинала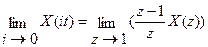

4. Теореме о запаздывании или смещении оригинала

Дискретная передаточная функция.

 

 

 

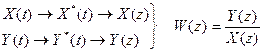
Дискретную передаточную функцию можно получить через импульсную переходную характеристику.

Подстановка Тастина.