Вероятность как функция события
Рассмотрим пространство элементарных (полную группу попарно несовместных) равновозможных событий  и рассмотри систему событий S, состоящую из невозможного события
и рассмотри систему событий S, состоящую из невозможного события  , всех событий
, всех событий  пространства G и всех событий А, которые могут быть подразделены на частные случаи, входящие в состав пространства G.
пространства G и всех событий А, которые могут быть подразделены на частные случаи, входящие в состав пространства G.
Пример. Если  , то
, то
 .
.
Лемма. Система S является полем событий.
Доказательство. Сумма, разность и произведение событий из S входят в S (перебор случаев для  ); невозможное событие
); невозможное событие  входит в S по определению, а достоверное событие входит в S, так как оно представляется в виде
входит в S по определению, а достоверное событие входит в S, так как оно представляется в виде  .Лемма доказана.
.Лемма доказана.
В соответствии с приведённым определением каждому событию А, принадлежащему к построенному полю событий S, приписывается вероятность  , где
, где 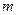 есть число тех событий
есть число тех событий  исходной группы G, которые являются частными случаями события А. Таким образом, вероятность
исходной группы G, которые являются частными случаями события А. Таким образом, вероятность  можно рассматривать как функцию от события А, определенную на поле событий S.
можно рассматривать как функцию от события А, определенную на поле событий S.