Частота события. Статистическая вероятность

Замечание. Далеко не всякий опыт может быть сведён к схеме случаев. Существует обширный класс событий, вероятности которых нельзя вычислить по формуле (2.1).

Примеры. 1) Несимметричная игральная кость.

2) Несимметричная монета.

3) Попадание в цель при выстреле.

4) Пробивание брони осколком снаряда и т.п.

Вместе с тем каждое из перечисленных событий обладает определённой степенью объективной возможности, которую в принципе можно измерить численно и которая при повторении подобных опытов будет отражаться в относительной частоте соответствующих событий.

Будем считать, что каждое событие, связанное с массой однородных опытов, - сводящееся к схеме случаев или нет, - имеет определённую вероятность, заключающуюся между нулём и единицей. Для событий, сводящихся к схеме случаев, эта вероятность может быть вычислена по формуле (2.1). Для событий, не сводящихся к схеме случаев, применяются другие способы определения вероятностей. Все эти способы основаны на эксперименте (опыте).

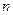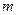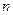Определение 1.Если проведена серия из опытов, в каждом из которых могло появиться или не появиться некоторое событие , то частотой события (статистической вероятностью события ) в данной серии опытов называется отношение числа опытов, в которых появилось событие , к общему числу произведённых опытов: . (3.1)

Замечание 1. При небольшом числе опытов частота события носит в значительной мере случайный характер и может заметно меняться от одной группы опытов к другой. Однако при увеличении числа опытов частота стабилизируется, приближаясь с незначительными колебаниями к некоторой средней, постоянной величине. Это свойство устойчивости частот, многократно проверенное на опытах, есть одна из наиболее характерных закономерностей, наблюдаемых в случайных явлениях. Проверить этот факт на практике можно только для событий, сводящихся к схеме случаев, так как только для этих событий существует точный способ вычисления математической вероятности. Многочисленные опыты этот факт действительно подтверждают.

Пример (опыт Бюффона и Пирсона). Бросание симметричной монеты.

Число бросаний	Число выпадений герба	Частота выпадений герба
		0,5080
		0,5016
		0,5005

Вполне естественно допустить, что и для событий, не сводящихся к схеме случаев, тот же закон остаётся в силе и что постоянное значение, к которому при увеличении числа опытов приближается частота наступления события, представляет собой вероятность события. Тогда частоту события при достаточно большом числе опытов можно принять за приближенное значение вероятности

Математическую формулировку и доказательство этого факта представил Я. Бернулли. Он доказал, что при неограниченном увеличении числа однородных независимых опытов с практической достоверностью можно утверждать, что частота события будет сколь угодно мало отличаться от его вероятности в отдельном опыте.

Замечание 2. Характер приближения частоты к вероятности при увеличении числа опытов отличается от стремления к пределу в математическом смысле.

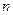В математическом анализе означает, что разность становится меньше любого положительного числа для всех значений , начиная с некоторого достаточно большого числа.

При экспериментальном определении вероятности через частоту события нет ничего физически невозможного в том, что при большом числе опытов частота события будет значительно уклоняться от его вероятности; но такое значительное уклонение является весьма маловероятным;тем менее вероятным, чем большее число опытов произведено. Пример: монета. Таким образом, при возрастании числа опытов частота приближается к вероятности, но не с полной достоверностью, а с большой вероятностью, которая при большом числе опытов может рассматриваться как практическая достоверность.

Определение 2. Говорят, что величина сходится по вероятности к величине 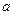, если при сколь угодно малом вероятность неравенства при увеличении 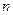неограниченно приближается к 1:

.

Замечание.Применяя этот термин, можно сказать, что при увеличении числа опытов частота события сходится по вероятности к вероятности события.