Пример. Выбор оптимального маршрута перевозки грузов
Математический аппарат ДП, основанный на методологии пошаговой оптимизации, может быть использован при нахождении кратчайших расстояний, например, на географической карте, представленной в виде сети.
Решение задачи по определению кратчайших расстояний между пунктами отправления и пунктами получения продукции по существующей транспортной сети является исходным этапом при решении таких экономических задач, как оптимальное прикрепление потребителей за поставщиками, повышение производительности транспорта за счёт сокращения непроизводительного пробега и др.
Пусть транспортная сеть состоит из 10 узлов, часть из которых соединены магистралями. На рис.3 показана сеть дорог и стоимости перевозки единицы груза между отдельными пунктами сети, которые проставлены у соответствующих рёбер. Необходимо определить маршрут доставки груза из пункта 1 в пункт 10, обеспечивающий наименьшие транспортные расходы (Fk (i)).
Аналогичная задача может быть поставлена для оптимизации технологического маршрута изготовления изделия (технологии перевалки груза), если на сети маршрутов задаться трудоемкостью или стоимостью каждой технологической операции. Искомый путь может быть найден интуитивно, а затем его можно сравнить с полученным оптимальным решением.
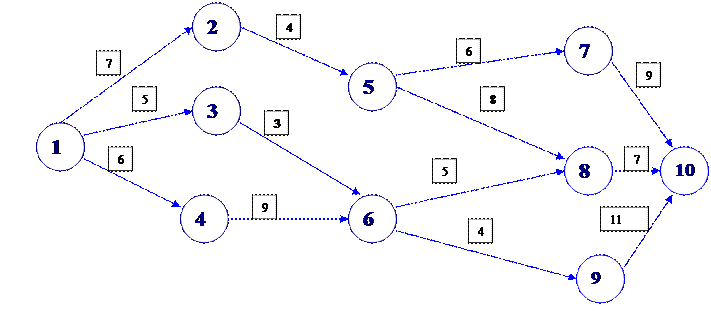
 Рисунок 3 - Модель транспортной сети
Рисунок 3 - Модель транспортной сети
В основе решения задач ДП лежит принцип оптимальности Беллмана:
на каждом этапе принимается такое решение, которое обеспечивает оптимального с данного этапа до конца процесса, то есть на каждом этапе необходимо принимать решение, просматривая его последствия до самого конца.
А так как последовательность решения следует просматривать до конца процесса, то варианты анализируют, начиная с конца процесса.
Решение. В задаче имеется ограничения – двигаться по изображенным на схеме маршрутам можно только слева на право, т.е. попав, например, в пункт 7, мы имеем право переместится только в пункт 10, и не можем возвратиться обратно в пункт 5 или пункт 6.
Эта особенность транспортной сети даёт право отнести каждый из 10-ти пунктов к одному из поясов. Будем считать, что пункт принадлежит k- му поясу, если из него попасть в конечный пункт ровно за k шагов, т.е. с заездом ровно в (k - 1)-й промежуточный пункт.
Таким образом, пункты 7, 8 и 9 принадлежат к первому поясу, пункты 5 и 6 ко второму, пункты 2, 3 и 4 к третьему и пункт 1 к четвёртому.
Тогда на k- м шаге будем находить оптимальные маршруты перевозки груза из пунктов k- го пояса до конечного пункта.
Оптимизацию будем производить с конца процесса, и потому, дойдя до k- го шага, неизвестно, в каком из пунктов k- го пояса окажется груз, перевозимый из первого пункта.
Введём обозначения:
· k- номер шага (k= 1, 2, 3, 4);
· i - пункт, из которого осуществляются перевозки (i= 1,2,…,9)
· j- пункт, в который доставляется груз (j= 2,3,…,10)
· Cij- стоимость перевозки груза из пункта i в пункт j.
· Fk (i)- минимальные затраты на перевозку груза на k- м шаге решения задачи из пункта i до конечного пункта.
Очевидно, что минимум затрат на перевозку груза из пунктов k- го пояса до пункта 10 будет зависеть от того, в каком пункте пояса мы оказались. Номер i пункта, принадлежащего k-му поясу, будет являться переменной состояния системы на k- м шаге.
Для первого шага управления (k=1) функция Беллмана представляет собой минимальные затраты на перевозку груза из пунктов 1-го пояса в конечный пункт, т.е. F1(i) = Сi10. Для последующих шагов затраты складываются из двух слагаемых – стоимости перевозки груза Cij из пункта i k- го пояса в пункт j (k-1)-го пояса и минимально возможных затрат на перевозку из пункта j до конечного пункта, т.е. Fk-1 (j). Таким образом, функциональное уравнение Беллмана будет иметь вид
Fk (i)= min { Cij+ Fk-1 (j) } (11)
Минимум затрат достигается на некотором значении j*, которое является оптимальным направлением движения из пункта i в конечный пункт.
На четвёртом шаге попадаем на 4-ыйй пояс и состояния системы становится определённым i=1. Функция F4 (1)представляет собой минимально возможные затраты по перемещению груза из 1-го пункта в 10-й.
Оптимальный маршрут определяется в результате анализа всех шагов в обратном порядке, а выбор некоторого управления j на k- м шаге приводит к тому, что состояние системы на (k-1)-м шаге становится определённым.