Динамическое программирование транспортных процессов.

Задача о кратчайшем пути

Задача о максимальном потоке

Таблица 2 - Основные временные параметры сетевых графиков

Элемент сети, характеризуемый параметром	Наименование параметра	Условное обозначение
Событие (і)	Ранний срок свершения события	t_p (i)
Поздний срок свершения события	t_п (i)
Резерв времени события	R (i)
Работа (і,j)	Продолжительность работы	t (i,j)
Полный резерв времени работы	R_п (i,j)
Частный резерв первого вида	R₁ (i,j)
Частный резерв второго вида	R₂ (i,j)
Независимый резерв времени работы	R_н (i,j)
Путь (L)	Продолжительность пути	t (L)
Продолжительность критического пути	t_кp
Резерв времени пути	R(L)

Расчет параметров события.

Событие не может наступить раньше, чем осуществятся все предшествующие ему работы. Поэтому ранний (или ожидаемый) срок t_p(i) свершения і-ого события определяется продолжительностью максимального пути, который предшествует этому событию:

t_p(i) = max t (L_пі) (1)

L_пі

где L_пі - любой путь, который предшествует і-ому событию, то есть путь от исходного к і-ому событию сети.

Если событие имеет несколько предшествующих путей, а также несколько предшествующих событий, то ранний срок свершения события удобно находить по формуле:

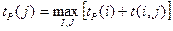(2)

Поздний (или предельный) срок t_п(i) свершения i-ого события рассчитывается по формуле: ( Понятия в методичке!!!)

t_п (i) = t_кр - max (L_cі), (3)

где L_cі- любой путь, который следует за і-ым событием, то есть путь от і-ого к завершающему событию сети.

Если событие i имеет несколько последующих путей, а также несколько последующих событий, то поздний срок свершения события удобно находить по формуле:

(4)

Резерв времени R(i) i-ого события определяется как разность между поздним и ранним сроками его свершения:

R (i) = t_п (i) - t_p (i) (5)

Резерв времени события показывает, на какой допустимый период времени можно задержать наступления этого события, не вызывая при этом увеличение срока выполнение всего комплекса работ.

Критические события резервов времени не имеют, так как любая задержка в свершении события, которые лежит на критическом пути, вызовет такую же задержку в свершении завершающего события, а следовательно, и всего комплекса работ по проекту.

Из этого следует, что для того, чтобы определить длину и топологию критического пути, совсем не обязательно перебирать все полные пути и определять их продолжительность. Определив ранний срок свершения завершающего события сети, мы тем самим определяем продолжительность критического пути, а обнаружив события с нулевыми резервами времени, определяем его топологию.

Расчет основных параметров работы.

Прежде чем рассматривать резервы времени работ, обратимся к резерву времени пути. Такие резервы имеют все некритические пути. Резерв времени пути R(L) определяется как разность между продолжительностью критического и рассматриваемого пути:

R (L)=t_кр – t (L). (6)

Он показывает, на какую величину могут быть увеличены продолжительности всех работ, которые лежат на этом пути. Если затянуть выполнение работ, которые лежат на этом пути, на время большее чем R(L), то критический путь переместится на путь L.

Отсюда можно сделать вывод, что любая из работ пути L на его участке, которая не совпадает с критическим путем (замкнутым между двумя событиями критического пути), имеет резерв времени.

ВСЕ ЭТО ОБЯЗАТЕЛЬНО ПОЧИТАТЬ В МЕТОДИЧКЕ!!!!!!!

Полный резерв времени R_п (i,j) работы (i,j)показывает, как можно увеличить время выполнения данной работы при условии, что срок выполнения всего комплекса работ не изменится:

R_п (i,j) = t_п (j) - t_p (i) - t (i,j) (7)

Частный резерв времени первого вида R₁(i,j) работы (i,j) - часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока свершения ее начального события. Этим резервом можно располагать при выполнении данной работы в предположении, что ее начальное и конечное события свершаются в свои самые поздние сроки.

R₁ (i,j) = t_п (j) - t_п (i) - t (i,j) (8)

Частный резерв времени второго вида или свободный резерв времени работы R₂ (i,j) - часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока свершения ее конечного события. Этим резервом можно располагать при выполнении данной работы в предположении, что ее начальное и конечное события свершатся в свои самые ранние сроки:

R₂ (i,j) = t_p (j) - t_p (i) - t (i,j) (9)

Свободным резервом времени можно пользоваться для предотвращения случаев, которые могут возникнуть в ходе выполнения работ. Если планировать выполнения работ с ранними сроками их начала и окончания, то всегда будет возможность при необходимости перейти на поздние сроки начала и окончания работ.

Независимый резерв времени работы R_н (i,j) - часть полного резерва времени, получаемая для случая, если все предшествующие работы заканчиваются в поздний срок, а все последующие работы начинаются в ранний срок:

R_н (i,j) = t_p (j) - t_п (i) - t (i,j) (10)

Использование независимого резерва времени не влияет на величину резервов времени других работ.

Таким образом, если R₁ (i,j) может быть использован на увеличение продолжительности данной и последующей работ без затрат резерва времени предшествующих работ, а R₂ (i,j) - на увеличение продолжительности данной и предшествующих работ без нарушения резерва времени последующих работ, то R_н (i,j) может быть использован для увеличения продолжительности только данной работы.

Работы, которые лежат на критическом пути, равно как и критические события, резервов времени не имеют.

Если на критическом пути лежит начальное событие i, то R_п (i,j) = R₁ (i,j).

Если на критическом пути лежит конечное событие j, то R_п (i,j) = R₂ (i,j)

Если на критическом пути лежат начальное и конечное события, но самая работа не належит этому пути, то R_п (i,j) = R₁ (i,j) = R₂(i,j) = R_н (i,j).

Эти соотношения можно использовать при проверке правильности расчетов резервов времени отдельных работ.

Следует отметить, что классический вид сетевого графика - это сеть, начерченная без масштаба времени. Поэтому сетевой график, хотя и дает четкое представление о порядке выполнения работ, но недостаточно наглядный для определения тех работ, которые должны выполняться в каждый данный момент времени. В связи с этим проект после упорядоченного сетевого графика рекомендуется дополнить линейной диаграммой проекта (диаграммой Гантта).

Преимущество СПУ состоит в следующем:

1. концентрирует внимание руководителей на небольшом числе работ и исполнителей;

2. устанавливает четкую взаимосвязь между исполнителями, обеспечивая тесное организационное единство;

3. разрешает в любой момент времени располагать исчерпывающей информацией;

4. обеспечивает непрерывность управления ходом работ, своевременность принятия решений, оперативность вмешательства;

5. разрешает рационально маневрировать выделенными ресурсами;

6. дает большую экономию времени, средств, энергии, материалов и т.п.;

7. дисциплинирует исполнителей, создает объективную картину качества работ, доступных любому, исключая штурмовщину;

8. создается возможность выполнения вычислительных работ на компьютере.

В данное время методами СПУ решается около 14% задач общего объема применяемых математических методов. Работы по использованию и развитию СПУ получили широкое распространение в разных областях народного хозяйства нашей страны и за границей, накоплен большой опыт и своя история.

Методы и модели СПУ могут с успехом применяться в коммерческой деятельности при выполнении разных комплексов работ при:

· проведении текущего или капитального ремонта;

· реконструкции коммерческих торговых предприятий;

· подготовке и проведении оптовых и розничных ярмарок;

· разработке плана коммерческой деятельности;

· оперативной реконструкции секций супермаркетов;

· строительстве универсальных оптовых предприятий;

· разработке плана развития торговой сети;

· планировании торговой деятельности;

· составлении бухгалтерского отчета;

· снабжении товаров покупателям;

_·заключении договоров на снабжение;

_·открытии нового торгового предприятия,

_·выполнении многих комплексов финансово-коммерческих операций.

Пусть имеется некоторая сеть с заданной пропускной способностью дуг d_ij из i-ого узла в j-ый узел. Необходимо так организовать перевозки, чтобы перевезти максимальное количество груза из начального узла сети в конечный узел.

Обозначим x_ij– количество перевозимого груза из i-ого пункта в j-ый пункт (i,j=1,…,n).

Экономико-математическая модель задачи:

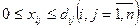Ограничение означает, что количество поступившего груза должно быть равно количеству вывезенного груза.

Пусть имеется сеть с источником S и стоком t. Известно расстояние между i-ым и j-ым узлами – c_ij. Необходимо найти кратчайший путь от начального узла до конечного узла.

Обозначим через x_ij булевую переменную, которая равна 1, если узел принадлежит кратчайшему пути, и 0 – в противном случае.

Экономико-математическая модель задачи:

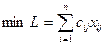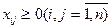Первое ограничение означает, что единица потока вытекает из источника S; второе ограничение – что единица потока втекает в сток t; третье ограничение гарантирует сохранение потока при протекании по сети.

До сих пор рассматривались такие задачи оптимизации, в которых принятие решения осуществлялось в один этап. Зависимость рассматриваемого этапа от прошлого и его влияние на будущее не учитывалось.

В реальных задачах управления приходиться принимать и реализовывать решения по нескольким этапам. Такие задачи многоэтапной оптимизации называют задачами динамического программирования (ДП), в том числе:

· распределение ресурсов, например, ограниченного объема капиталовложений между возможными направлениями их использования по объему и времени;

· разработка правил управления запасами, устанавливающих момент пополнения и размер пополняемого запаса;

· выбор транспортных маршрутов или технологических способов изготовления изделий;

· разработка принципов календарного планирования производства.