Теорема о существовании решения (теорема Пеано).

Доказательство теоремы существования решения задачи Коши.

Рассмотрим задачу Коши

, (1)

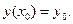(2)

 

Приведём ещё раз формулировку теоремы

Пусть функция задана на множествеи непрерывна на этом множестве по и . Тогда существует по крайней мере одно решение уравнения (1), удовлетворяющее условию (2), и это решение определено по крайней мере на отрезке , где , причём

Доказательство.По числам и определим числа и , указанные в формулировке теоремы. Ограничимся доказательством существования решения задачи Коши (1)-(2) на отрезке . Доказательство существования решения на отрезке проводится аналогично.

Введём множество 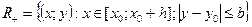. Построим на отрезке последовательность ломаных Эйлера следующим образом. Первая ломаная Эйлера будет состоять из одного звена:

.

Для построения второй ломаной разобьём отрезок на две равные части и построим ломаную Эйлера из двух звеньев:

.

Далее разобьём отрезок на три равные части и построим ломаную из трёх звеньев и т. д. На-м шаге отрезок разбивается на равных частей:

.

Величина называется шагом ломаной . Ломаная Эйлера будет иметь вид:

. (3)

Величины будут вычисляться по формулам

Все построенные ломаные будут целиком лежать в области 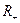. Действительно, в силу леммы, доказанной в предыдущем параграфе, мы имеем оценку

при ,

поскольку угловые коэффициенты звеньев всех ломаных суть величины , и следовательно, все они заключены между числами и по условию теоремы. Отсюда следует, что

а значит,

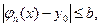если

Покажем теперь, что построенная последовательность ломаных Эйлера удовлетворяет теореме Арцела. Действительно, если , то для любого верна оценка

,

следовательно, все функции равномерно ограничены на отрезке . Далее, согласно лемме о хорде ломаной, для любых значений и из отрезка получим

.

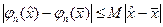Тогда для всякого и всякого натурального будет , если только

. Это означает, что все функции равностепенно непрерывны на отрезке . Тогда по теореме Арцела из последовательности можно выбрать подпоследовательность , равномерно сходящуюся на этом отрезке.

Замечание.В соответствии с теоремой Арцела, указанная подпоследовательность, может быть выбрана, вообще говоря, не единственным образом.

Пусть указанная подпоследовательность выбрана. Обозначим её предельную функцию через . Функция будет непрерывна на отрезке , не выйдет из множества 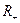и будет удовлетворять условию (2). Это следует из равномерной сходимости выбранной подпоследовательности и того, что все функции , построенные по формулам (3), проходят через точку .

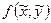Далее, чтобы убедиться, что функция является решением уравнения (1) на отрезке , покажем, что она имеет производную в любой точке этого отрезка и что эта производная равна значению, где .

Возьмём произвольное . Функция по условию теоремы непрерывна в точке , тогда существует такое число 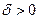, что для всех точек квадрата

будет выполнено условие

. (4)

Обозначим . Зафиксируем приращение , такое что .

Выберем число таким, чтобы для всех номеров 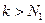выполнялись два условия:

• справедливо неравенство если (5)
• расстояние между абсциссами соседних угловых точек ломаной было бы меньше величины .

Такое число всегда найдётся. Действительно, неравенство (5) удовлетворяется, поскольку подпоследовательность , равномерно сходится на отрезке. Для выполнения второго требования достаточно взять , поскольку расстояние между абсциссами угловых точек ломаной есть .

Будем далее рассматривать только те ломаные , для которых 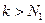. Покажем, что все угловые точки таких ломаных, лежат внутри квадрата , если только абсциссы этих угловых точек заключены между величинами и . Пусть сначала . По выбору и на основании леммы получим

если .

Переходя здесь к пределу при , получим

если .

Учитывая неравенство (5) при 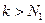будем иметь

, если .

Если , то левая часть отрезка заключена между соседними абсциссами угловых точек . Но при 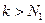выполнено , а тогда

Принимая во внимание сделанные оценки, окончательно получим

Таким образом, при 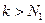все угловые точки ломаных лежат внутри квадрата , если только абсциссы этих угловых точек заключены между величинами и . Но тогда угловые коэффициенты всех этих звеньев, согласно условию (4), заключены между значениями и . Тогда по лемме о хорде ломаной будем иметь

,

следовательно

.

Рассмотрим модуль разности

Выберем теперь число таким, чтобы для всех номеров выполнялось условие если . Тогда при будем иметь

(6)

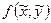где - фиксированное достаточно малое число. Итак, неравенством (6) показано что функция имеет производную в любой точке отрезка и эта производная равна значению, где . Следовательно, функция является решением уравнения (1) на отрезке . Теорема доказана.